《2025年星推荐涂教材高中数学选择性必修第三册人教版》

例 1 - 1
某地最近出台一项机动车驾照考试规定：每位考试者一年之内最多有 $4$ 次参加考试的机会，一旦某次考试通过，便可领取驾照，不再参加以后的考试，否则就一直考到第 $4$ 次为止。如果小李决定参加驾照考试，设他每次参加考试通过的概率依次为 $0.6$，$0.7$，$0.8$，$0.9$，求在一年内小李参加驾照考试次数 $\xi$ 的分布列和均值，并求小李在一年内领到驾照的概率。

答案：

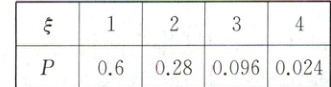
[名师讲习] 解：$\xi$ 的所有可能取值为 $1$，$2$，$3$，$4$。

$\xi = 1$，表明小李第一次参加驾照考试就通过了，

故 $P(\xi = 1)=0.6$；

$\xi = 2$，表明小李在第一次考试未通过，第二次通过了，

故 $P(\xi = 2)=(1 - 0.6)× 0.7 = 0.28$；

$\xi = 3$，表明小李在第一、二次考试未通过，第三次通过了，

故 $P(\xi = 3)=(1 - 0.6)×(1 - 0.7)× 0.8 = 0.096$；

$\xi = 4$，表明小李第一、二、三次考试都未通过，前三次考试未通过，参加第四次考试，无论通过与否，相当于乘概率 $1$。

故 $P(\xi = 4)=(1 - 0.6)×(1 - 0.7)×(1 - 0.8)=0.024$。

则 $\xi$ 的分布列为

常常验证概率和为 $1$。

所以 $E(\xi)=1× 0.6 + 2× 0.28 + 3× 0.096 + 4× 0.024 = 1.544$。

小李在一年内领到驾照的概率为

$1-(1 - 0.6)×(1 - 0.7)×(1 - 0.8)×(1 - 0.9)=0.9976$。注意和“参加四次考试的概率”进行区分。