2025年星推荐涂教材高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年星推荐涂教材高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
6. (2025·浙江温州模拟)某投资公司在今年年初准备将 1000 万元投资到“低碳”项目上,现有两个“低碳”项目供选择:项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利 40%,也可能亏损 10%,且这两种情况发生的概率分别为 $\frac{3}{5}$ 和 $\frac{2}{5}$;项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利 50%,可能亏损 30%,也可能不赔不赚,且这三种情况发生的概率分别为 $\frac{3}{5}$,$\frac{1}{3}$,$\frac{1}{15}$.设按“项目一”和“项目二”投资的收益分别为 $\xi_{1}$ 万元和 $\xi_{2}$ 万元.
(1)试分别写出随机变量 $\xi_{1}$ 和 $\xi_{2}$ 的分布列;
(2)针对以上两个投资项目,请你从投资收益的角度,为投资公司选择一个合理的投资项目,并说明理由.
(1)试分别写出随机变量 $\xi_{1}$ 和 $\xi_{2}$ 的分布列;
(2)针对以上两个投资项目,请你从投资收益的角度,为投资公司选择一个合理的投资项目,并说明理由.
答案:
6.解:
(1)由题意可知,随机变量$\xi_1$和$\xi_2$的分布列分别为

(2)$E(\xi_1)=400×\frac{3}{5}+(-100)×\frac{2}{5}=200(万元)$,
$E(\xi_2)=500×\frac{3}{5}+(-300)×\frac{1}{3}+0×\frac{1}{15}=200(万元)$,
又$D(\xi_1)=(400 - 200)^{2}×\frac{3}{5}+(-100 - 200)^{2}×\frac{2}{5}=60000$,
$D(\xi_2)=(500 - 200)^{2}×\frac{3}{5}+(-300 - 200)^{2}×\frac{1}{3}+(0 -200)^{2}×\frac{1}{15}=140000$,
因为$E(\xi_1)=E(\xi_2),D(\xi_1)<D(\xi_2)$,说明项目一、项目二获
利的均值相等,但由于项目一的获利更稳定,所以该投资公司
投资项目一更合理.
6.解:
(1)由题意可知,随机变量$\xi_1$和$\xi_2$的分布列分别为

(2)$E(\xi_1)=400×\frac{3}{5}+(-100)×\frac{2}{5}=200(万元)$,
$E(\xi_2)=500×\frac{3}{5}+(-300)×\frac{1}{3}+0×\frac{1}{15}=200(万元)$,
又$D(\xi_1)=(400 - 200)^{2}×\frac{3}{5}+(-100 - 200)^{2}×\frac{2}{5}=60000$,
$D(\xi_2)=(500 - 200)^{2}×\frac{3}{5}+(-300 - 200)^{2}×\frac{1}{3}+(0 -200)^{2}×\frac{1}{15}=140000$,
因为$E(\xi_1)=E(\xi_2),D(\xi_1)<D(\xi_2)$,说明项目一、项目二获
利的均值相等,但由于项目一的获利更稳定,所以该投资公司
投资项目一更合理.
7. (2025·广东深圳模拟)新高考数学试卷出现多项选择题,每小题的四个选项中,全部选对得 6 分,部分选对得部分分,有选错的得 0 分.若正确答案为两项,每对一项得 3 分;若正确答案为三项,每对一项得 2 分.
(1)学生甲在作答某题时,对四个选项作出正确判断、判断不了(不选)和错误判断的概率如下表:
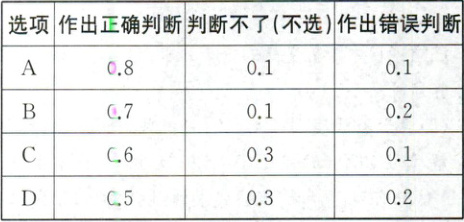
若此题的正确选项为 AC,求学生甲答此题得分 X 的分布列.
(2)某数学小组研究发现,多选题正确答案是两个选项的概率为 p,正确答案是三个选项的概率为 $1 - p(0\lt p\lt1)$.现有一道多选题,学生乙完全不会,此时他有两种答题方案:
方案一:随机选一个选项:方案二:随机选两个选项.
①若 $p=\frac{1}{2}$,且学生乙选择方案一,分别求学生乙本题得 0 分、得 2 分的概率.
②以本题得分的数学期望为决策依据,p 的取值在什么范围内唯独选择方案一最好?
(2)①分正确答案是两个或三个选项,利用古典概型求解;
②分别计算方案一、方案二的数学期望,列不等式求 p 的取值范围.
(1)学生甲在作答某题时,对四个选项作出正确判断、判断不了(不选)和错误判断的概率如下表:

若此题的正确选项为 AC,求学生甲答此题得分 X 的分布列.
(2)某数学小组研究发现,多选题正确答案是两个选项的概率为 p,正确答案是三个选项的概率为 $1 - p(0\lt p\lt1)$.现有一道多选题,学生乙完全不会,此时他有两种答题方案:
方案一:随机选一个选项:方案二:随机选两个选项.
①若 $p=\frac{1}{2}$,且学生乙选择方案一,分别求学生乙本题得 0 分、得 2 分的概率.
②以本题得分的数学期望为决策依据,p 的取值在什么范围内唯独选择方案一最好?
(2)①分正确答案是两个或三个选项,利用古典概型求解;
②分别计算方案一、方案二的数学期望,列不等式求 p 的取值范围.
答案:
7.解:
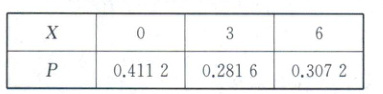
(1)因为正确选项为$AC$,所以$X$的可能取值为$0,3,6$,
得$3$分即只选对了$A$或只选对了$C$,
$P(X = 3)=0.8×(1 - 0.6)×(1 - 0.2)×(1 - 0.2)+(1 - 0.8)×0.6×(1 - 0.2)×(1 - 0.2)=0.2816$,
得$6$分即选对了$A$和$C$,且没选$B$和$D$,
$P(X = 6)=0.8×(0.7 + 0.1)×0.6×(0.5 + 0.3)=0.3072$.
所以$P(X = 0)=1 - 0.2816 - 0.3072 = 0.4112$.
所以学生甲答此题得分$X$的分布列为
(2)①记$X$为“从四个选项中随机选择一个选项的得分”,
$P(X = 0)=\frac{1}{2}×\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{4}^{2}}+\frac{1}{2}×\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{4}^{2}}=\frac{3}{8}$,
$P(X = 2)=\frac{1}{2}×\frac{\mathrm{C}_{3}^{3}}{\mathrm{C}_{4}^{2}}=\frac{3}{8}$
②对于方案一:记$\xi$为“从四个选项中随机选择一个选项的得
分”,则$\xi$的所有可能取值为$0,2,3$,则
$P(\xi = 0)=p×\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{4}^{2}}+(1 - p)×\frac{\mathrm{C}_{1}^{1}\mathrm{C}_{1}^{1}}{\mathrm{C}_{4}^{2}}=\frac{1 + p}{4}$,
$P(\xi = 2)=(1 - p)×\frac{\mathrm{C}_{3}^{3}}{\mathrm{C}_{4}^{2}}=\frac{3}{8}(1 - p)$,
$P(\xi = 3)=p×\frac{\mathrm{C}_{4}^{1}\mathrm{C}_{2}^{1}}{\mathrm{C}_{4}^{2}}=\frac{1}{2}p$.
所以$E(\xi)=0×\frac{1 + p}{4}+2×\frac{3}{8}(1 - p)+3×\frac{1}{2}p=\frac{3}{2}$.
对于方案二:记$\epsilon$为“从四个选项中随机选择两个选项的得
分”,则$\epsilon$的所有可能取值为$0,4,6$,则
$P(\epsilon = 0)=p×\frac{\mathrm{C}_{2}^{2}-1}{\mathrm{C}_{4}^{2}}+(1 - p)×\frac{\mathrm{C}_{3}^{1}\mathrm{C}_{1}^{1}}{\mathrm{C}_{4}^{2}}=\frac{1}{3}p+\frac{1}{2}$,
$P(\epsilon = 4)=(1 - p)×\frac{\mathrm{C}_{3}^{2}-1}{\mathrm{C}_{4}^{2}}=\frac{1}{2}(1 - p)$,
$P(\epsilon = 6)=p×\frac{1}{\mathrm{C}_{4}^{2}}=\frac{1}{6}p$.
所以$E(\epsilon)=0×(\frac{1}{3}p+\frac{1}{2})+4×\frac{1}{2}(1 - p)+6×\frac{1}{6}p=2 - p$.
要使唯独选择方案一最好,则$\begin{cases}2 - p<\frac{3}{2}\\0<p<1\end{cases}$,
解得$\frac{1}{2}<p<1$,故$p$的取值范围是$(\frac{1}{2},1)$.
7.解:
(1)因为正确选项为$AC$,所以$X$的可能取值为$0,3,6$,
得$3$分即只选对了$A$或只选对了$C$,
$P(X = 3)=0.8×(1 - 0.6)×(1 - 0.2)×(1 - 0.2)+(1 - 0.8)×0.6×(1 - 0.2)×(1 - 0.2)=0.2816$,
得$6$分即选对了$A$和$C$,且没选$B$和$D$,
$P(X = 6)=0.8×(0.7 + 0.1)×0.6×(0.5 + 0.3)=0.3072$.
所以$P(X = 0)=1 - 0.2816 - 0.3072 = 0.4112$.
所以学生甲答此题得分$X$的分布列为

(2)①记$X$为“从四个选项中随机选择一个选项的得分”,
$P(X = 0)=\frac{1}{2}×\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{4}^{2}}+\frac{1}{2}×\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{4}^{2}}=\frac{3}{8}$,
$P(X = 2)=\frac{1}{2}×\frac{\mathrm{C}_{3}^{3}}{\mathrm{C}_{4}^{2}}=\frac{3}{8}$
②对于方案一:记$\xi$为“从四个选项中随机选择一个选项的得
分”,则$\xi$的所有可能取值为$0,2,3$,则
$P(\xi = 0)=p×\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{4}^{2}}+(1 - p)×\frac{\mathrm{C}_{1}^{1}\mathrm{C}_{1}^{1}}{\mathrm{C}_{4}^{2}}=\frac{1 + p}{4}$,
$P(\xi = 2)=(1 - p)×\frac{\mathrm{C}_{3}^{3}}{\mathrm{C}_{4}^{2}}=\frac{3}{8}(1 - p)$,
$P(\xi = 3)=p×\frac{\mathrm{C}_{4}^{1}\mathrm{C}_{2}^{1}}{\mathrm{C}_{4}^{2}}=\frac{1}{2}p$.
所以$E(\xi)=0×\frac{1 + p}{4}+2×\frac{3}{8}(1 - p)+3×\frac{1}{2}p=\frac{3}{2}$.
对于方案二:记$\epsilon$为“从四个选项中随机选择两个选项的得
分”,则$\epsilon$的所有可能取值为$0,4,6$,则
$P(\epsilon = 0)=p×\frac{\mathrm{C}_{2}^{2}-1}{\mathrm{C}_{4}^{2}}+(1 - p)×\frac{\mathrm{C}_{3}^{1}\mathrm{C}_{1}^{1}}{\mathrm{C}_{4}^{2}}=\frac{1}{3}p+\frac{1}{2}$,
$P(\epsilon = 4)=(1 - p)×\frac{\mathrm{C}_{3}^{2}-1}{\mathrm{C}_{4}^{2}}=\frac{1}{2}(1 - p)$,
$P(\epsilon = 6)=p×\frac{1}{\mathrm{C}_{4}^{2}}=\frac{1}{6}p$.
所以$E(\epsilon)=0×(\frac{1}{3}p+\frac{1}{2})+4×\frac{1}{2}(1 - p)+6×\frac{1}{6}p=2 - p$.
要使唯独选择方案一最好,则$\begin{cases}2 - p<\frac{3}{2}\\0<p<1\end{cases}$,
解得$\frac{1}{2}<p<1$,故$p$的取值范围是$(\frac{1}{2},1)$.
查看更多完整答案,请扫码查看


