2025年星推荐涂教材高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年星推荐涂教材高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第121页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
14.某学校的功能室统一使用某品牌的一种灯管,已
知这种灯管的使用寿命(单位:月)服从正态分布
N(μ,σ²),且使用寿命不少于12个月的概率为
0.8,使用寿命不少于24个月的概率为0.2.
(1)求这种灯管的平均使用寿命μ;
(2)假设一间功能室一次性换上4支这种新灯管,使用12个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少有两支灯管需要更换的概率. 利用对立事件的概率求解较简单.
知这种灯管的使用寿命(单位:月)服从正态分布
N(μ,σ²),且使用寿命不少于12个月的概率为
0.8,使用寿命不少于24个月的概率为0.2.
(1)求这种灯管的平均使用寿命μ;
(2)假设一间功能室一次性换上4支这种新灯管,使用12个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少有两支灯管需要更换的概率. 利用对立事件的概率求解较简单.
答案:
14.解:
(1)$\because \xi \sim N(\mu, \sigma^2)$,$P(\xi \geqslant 12) = 0.8$,$P(\xi \geqslant 24) = 0.2$,$\therefore P(\xi < 12) = 0.2$,显然$P(\xi < 12) = P(\xi \geqslant 24)$.
由正态曲线的对称性可知$\mu = \frac{12 + 24}{2} = 18$,即这种灯管的平均使用寿命是$18$个月.
(2)每支灯管使用$12$个月已经损坏的概率为$1 - 0.8 = 0.2$,假设使用$12$个月时该功能室需要更换的灯管数量为$\eta$(单位:支),则$\eta \sim B(4, 0.2)$,故至少有两支灯管需要更换的概率$P = 1 - P(\eta = 0) - P(\eta = 1) = 1 - C_4^0 × 0.8^4 - C_4^1 × 0.8^3 × 0.2 = 0.1808$.
(1)$\because \xi \sim N(\mu, \sigma^2)$,$P(\xi \geqslant 12) = 0.8$,$P(\xi \geqslant 24) = 0.2$,$\therefore P(\xi < 12) = 0.2$,显然$P(\xi < 12) = P(\xi \geqslant 24)$.
由正态曲线的对称性可知$\mu = \frac{12 + 24}{2} = 18$,即这种灯管的平均使用寿命是$18$个月.
(2)每支灯管使用$12$个月已经损坏的概率为$1 - 0.8 = 0.2$,假设使用$12$个月时该功能室需要更换的灯管数量为$\eta$(单位:支),则$\eta \sim B(4, 0.2)$,故至少有两支灯管需要更换的概率$P = 1 - P(\eta = 0) - P(\eta = 1) = 1 - C_4^0 × 0.8^4 - C_4^1 × 0.8^3 × 0.2 = 0.1808$.
15.(2025.山东临沂模拟)某市为了传承发展中华优
秀传统文化,组织该市中学生进行了一次文化知识有奖竞赛(满分100分),竞赛奖励规则如下:得分在[70,80)内的学生获三等奖,得分在[80,90
内的学生获二等奖,得分在[90,100]内的学生获一
等奖,其他学生不得奖.为了解学生对相关知识的
掌握情况,随机抽取100名学生的竞赛成绩,并以
此为样本绘制了如图所示的样本频率分布直方图.
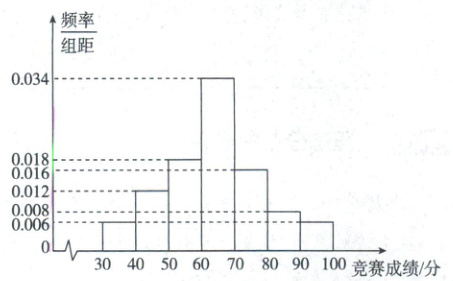
(1)现从该样本中随机抽取两名学生的竞赛成绩,
求这两名学生中恰有一名学生获奖的概率,.−C。
Co0
(2)若该市所有参赛学生的成绩X近似服从正态
分布N(μ,σ²),其中σ≈15,μ为样本平均数的估
计值,利用所得正态分布模型解决以下问题:取频中率,、再值求,和:
①若该市共有10000名学生参加了竞赛,试估计
参赛学生中成绩超过79分的学生数(结果精确到
整数);
②若从所有参赛学生中(参赛学生数大于10000)
随机抽取3名学生进行访谈,设其中竞赛成绩在
64分以上的学生数为令,求随机变量m的分布列和
均值. 服从二项分布:
附:若随机变量X服从正态分布N(μ,²),则P(μ一
σ<X<μ+σ)≈0.6827,P(μ−20<X<μ+2)
≈0.9545,P(μ−3子<X<μ+3σ)≈0.9973.
秀传统文化,组织该市中学生进行了一次文化知识有奖竞赛(满分100分),竞赛奖励规则如下:得分在[70,80)内的学生获三等奖,得分在[80,90
内的学生获二等奖,得分在[90,100]内的学生获一
等奖,其他学生不得奖.为了解学生对相关知识的
掌握情况,随机抽取100名学生的竞赛成绩,并以
此为样本绘制了如图所示的样本频率分布直方图.

(1)现从该样本中随机抽取两名学生的竞赛成绩,
求这两名学生中恰有一名学生获奖的概率,.−C。
Co0
(2)若该市所有参赛学生的成绩X近似服从正态
分布N(μ,σ²),其中σ≈15,μ为样本平均数的估
计值,利用所得正态分布模型解决以下问题:取频中率,、再值求,和:
①若该市共有10000名学生参加了竞赛,试估计
参赛学生中成绩超过79分的学生数(结果精确到
整数);
②若从所有参赛学生中(参赛学生数大于10000)
随机抽取3名学生进行访谈,设其中竞赛成绩在
64分以上的学生数为令,求随机变量m的分布列和
均值. 服从二项分布:
附:若随机变量X服从正态分布N(μ,²),则P(μ一
σ<X<μ+σ)≈0.6827,P(μ−20<X<μ+2)
≈0.9545,P(μ−3子<X<μ+3σ)≈0.9973.
答案:
15.解:
(1)由题意知,样本中学生获奖的概率为$0.16 + 0.08 + 0.06 = 0.3$,所以样本中有$30$人获奖,$70$人没有获奖.
则现从该样本中随机抽取两名学生的竞赛成绩,这两名学生中恰有一名学生获奖的概率为$\frac{C_{30}^1 C_{70}^1}{C_{100}^2} = \frac{14}{33}$.
(2)①$\mu = 10 × (35 × 0.006 + 45 × 0.012 + 55 × 0.018 + 65 × 0.034 + 75 × 0.016 + 85 × 0.008 + 95 × 0.006) = 64$,所以$X$近似服从正态分布$N(64, 15^2)$,故$P(64 - 15 \leqslant X \leqslant 64 + 15) \approx 0.6827$,所以$P(79 < X \leqslant 100) = \frac{1}{2}[1 - P(64 - 15 \leqslant X \leqslant 64 + 15)] \approx \frac{1}{2} × (1 - 0.6827) = 0.15865$,所以$10000 × 0.15865 = 1586.5 \approx 1587$,故估计该市参赛学生中成绩超过$79$分的学生数为$1587$.
②因为竞赛成绩的均值为$64$分,故$64$分以上的学生数$\xi \sim B(3, \frac{1}{2})$,所以$P(\xi = 0) = C_3^0 (\frac{1}{2})^3 = \frac{1}{8}$,$P(\xi = 1) = C_3^1 (\frac{1}{2})^3 = \frac{3}{8}$,$P(\xi = 2) = C_3^2 (\frac{1}{2})^3 = \frac{3}{8}$,$P(\xi = 3) = C_3^3 (\frac{1}{2})^3 = \frac{1}{8}$,所以随机变量$\xi$的分布列为
$\xi$ 0 1 2 3
$P$ $\frac{1}{8}$ $\frac{3}{8}$ $\frac{3}{8}$ $\frac{1}{8}$
故$E(\xi) = 0 × \frac{1}{8} + 1 × \frac{3}{8} + 2 × \frac{3}{8} + 3 × \frac{1}{8} = \frac{3}{2}$(或$E(\xi) = 3 × \frac{1}{2} = \frac{3}{2}$).
(1)由题意知,样本中学生获奖的概率为$0.16 + 0.08 + 0.06 = 0.3$,所以样本中有$30$人获奖,$70$人没有获奖.
则现从该样本中随机抽取两名学生的竞赛成绩,这两名学生中恰有一名学生获奖的概率为$\frac{C_{30}^1 C_{70}^1}{C_{100}^2} = \frac{14}{33}$.
(2)①$\mu = 10 × (35 × 0.006 + 45 × 0.012 + 55 × 0.018 + 65 × 0.034 + 75 × 0.016 + 85 × 0.008 + 95 × 0.006) = 64$,所以$X$近似服从正态分布$N(64, 15^2)$,故$P(64 - 15 \leqslant X \leqslant 64 + 15) \approx 0.6827$,所以$P(79 < X \leqslant 100) = \frac{1}{2}[1 - P(64 - 15 \leqslant X \leqslant 64 + 15)] \approx \frac{1}{2} × (1 - 0.6827) = 0.15865$,所以$10000 × 0.15865 = 1586.5 \approx 1587$,故估计该市参赛学生中成绩超过$79$分的学生数为$1587$.
②因为竞赛成绩的均值为$64$分,故$64$分以上的学生数$\xi \sim B(3, \frac{1}{2})$,所以$P(\xi = 0) = C_3^0 (\frac{1}{2})^3 = \frac{1}{8}$,$P(\xi = 1) = C_3^1 (\frac{1}{2})^3 = \frac{3}{8}$,$P(\xi = 2) = C_3^2 (\frac{1}{2})^3 = \frac{3}{8}$,$P(\xi = 3) = C_3^3 (\frac{1}{2})^3 = \frac{1}{8}$,所以随机变量$\xi$的分布列为
$\xi$ 0 1 2 3
$P$ $\frac{1}{8}$ $\frac{3}{8}$ $\frac{3}{8}$ $\frac{1}{8}$
故$E(\xi) = 0 × \frac{1}{8} + 1 × \frac{3}{8} + 2 × \frac{3}{8} + 3 × \frac{1}{8} = \frac{3}{2}$(或$E(\xi) = 3 × \frac{1}{2} = \frac{3}{2}$).
查看更多完整答案,请扫码查看


