2025年星推荐涂教材高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年星推荐涂教材高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
2. (2025·湖北黄冈月考)证明:$ 1 + \frac{1}{2}C_{n}^{1} + \frac{1}{3}C_{n}^{2} + ·s + \frac{1}{n + 1}C_{n}^{n} = \frac{1}{n + 1}(C_{n + 1}^{1} + C_{n + 1}^{2} + ·s + C_{n + 1}^{n + 1}) $。
通项是 $ \frac{1}{m}C_{n}^{m - 1} $。
通项是 $ \frac{1}{m}C_{n}^{m - 1} $。
答案:
2.证明:因为$\frac{1}{m}$Cₙᵐ⁻¹ = $\frac{n!}{m·(m - 1)!·(n - m + 1)!}$ = $\frac{n!}{(n + 1)!}$·$\frac{n + 1}{n - m + 1}$ = $\frac{1}{n + 1}$Cₙ₊₁ᵐ,当m = 1,2,3,…,n + 1时,分别代入相加,得1 + $\frac{1}{2}$Cₙ₊₁² + $\frac{1}{3}$Cₙ₊₁³ + … + $\frac{1}{n + 1}$Cₙ₊₁ⁿ⁺¹ = $\frac{1}{n + 1}$(Cₙ₊₁¹ + Cₙ₊₁² + … + Cₙ₊₁ⁿ⁺¹)。故原命题得证。
3. (2025·吉林长春模拟)为了配合创建全国文明城市的活动,某校现从 4 名男教师和 5 名女教师中选取 3 人组成文明志愿者小组,若男女至少各有一人,则不同的选法共有(
A.140 种
B.84 种
C.70 种
D.35 种
C
)A.140 种
B.84 种
C.70 种
D.35 种
答案:
3.C解析:方法一(直接法):可按选取男教师的人数分两类。第一类:从9名教师中选1名男教师和2名女教师,共有C₉¹C₅²种选法;第二类:从9名教师中选2名男教师和1名女教师,共有C₉²C₅¹种选法。根据分类加法计数原理得不同的选法种数为C₉¹C₅² + C₉²C₅¹ = 70。
方法二(间接法):从4名男教师和5名女教师中选取3人,共有C₉³种选法。若全为男教师,共有C₄³种选法;若全为女教师,共有C₅³种选法。所以若男女至少各有一人,则不同的选法种数为C₉³ - C₄³ - C₅³ = 70。故选C。
方法二(间接法):从4名男教师和5名女教师中选取3人,共有C₉³种选法。若全为男教师,共有C₄³种选法;若全为女教师,共有C₅³种选法。所以若男女至少各有一人,则不同的选法种数为C₉³ - C₄³ - C₅³ = 70。故选C。
4. 某中学高三学习雷锋志愿小组共有 16 人,其中一班、二班、三班、四班各 4 人,现从中任选 3 人,要求这三人不能全是同一个班的学生,且三班至多选 1 人,则不同选法的种数为可以有同班的。(
A.484
B.472
C.252
D.232
B
)A.484
B.472
C.252
D.232
答案:
4.B解析:以是否选择三班的学生为标准分为两类,每个类别又按是否选自同一个班分成两类,如表所示。
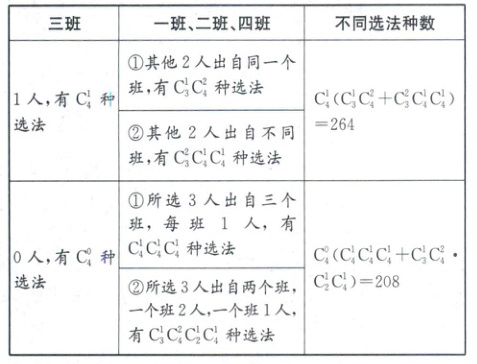
所以不同选法的种数为264 + 208 = 472。故选B。
4.B解析:以是否选择三班的学生为标准分为两类,每个类别又按是否选自同一个班分成两类,如表所示。

所以不同选法的种数为264 + 208 = 472。故选B。
5. (2025·湖北武汉联考)某人决定投资 8 种股票和 4 种债券,若经纪人向他推荐 12 种股票和 7 种债券,则此人不同的投资方式的种数为(
A.$ A_{12}^{8} · A_{7}^{4} $
B.$ C_{12}^{8} · C_{7}^{4} $
C.$ A_{12}^{8} + A_{7}^{4} $
D.$ C_{12}^{8} + C_{7}^{4} $
B
)A.$ A_{12}^{8} · A_{7}^{4} $
B.$ C_{12}^{8} · C_{7}^{4} $
C.$ A_{12}^{8} + A_{7}^{4} $
D.$ C_{12}^{8} + C_{7}^{4} $
答案:
5.B解析:完成这件事需分两步:第一步,根据经纪人的推荐在12种股票中选8种,有C₁₂⁸种选法;第二步,根据经纪人的推荐在7种债券中选4种,有C₇⁴种选法。根据分步乘法计数原理,此人有C₁₂⁸·C₇⁴种不同的投资方式。
6. (2025·湖南衡阳检测)某医院有内科医生 12 名,外科医生 8 名,现选派 5 名参加研讨会。
(1)若内科医生甲与外科医生乙必须参加,则共有多少种不同的选法?“含”的问题。
(2)甲、乙均不能参加,有多少种不同的选法?“不含”的问题。
解题通法
“含……”或“不含……”是组合应用的常见题型。其解决方法一般为直接分步法,即“含”的先取出,“不含”的可把特殊对象去掉再取出,分步计数。
必要时,还需对对象进行分类,对题目中的对象分类后,要弄清被取出的对象“含有”哪一类,“含有”多少个,或者对于某个特殊对象,被取出的对象中含不含这个特殊对象,这是解题的关键。
当用直接法分类较多时,可考虑用间接法处理,即“正难则反”的策略。
(1)若内科医生甲与外科医生乙必须参加,则共有多少种不同的选法?“含”的问题。
(2)甲、乙均不能参加,有多少种不同的选法?“不含”的问题。
解题通法
“含……”或“不含……”是组合应用的常见题型。其解决方法一般为直接分步法,即“含”的先取出,“不含”的可把特殊对象去掉再取出,分步计数。
必要时,还需对对象进行分类,对题目中的对象分类后,要弄清被取出的对象“含有”哪一类,“含有”多少个,或者对于某个特殊对象,被取出的对象中含不含这个特殊对象,这是解题的关键。
当用直接法分类较多时,可考虑用间接法处理,即“正难则反”的策略。
答案:
6.解:
(1)根据题意,内科医生甲与外科医生乙必须参加,则在剩下的18人中再选3人即可,有C₁₈³ = 816(种)不同的选法。
(2)甲、乙均不能参加,在剩下的18人中选5人即可,有C₁₈⁵ = 8568(种)不同的选法。
(1)根据题意,内科医生甲与外科医生乙必须参加,则在剩下的18人中再选3人即可,有C₁₈³ = 816(种)不同的选法。
(2)甲、乙均不能参加,在剩下的18人中选5人即可,有C₁₈⁵ = 8568(种)不同的选法。
7. (2025·辽宁沈阳单元测试)某车间有 11 名工人,其中 5 名男工是钳工,4 名女工是车工,另外 2 名老师傅既能当车工又能当钳工,现在要在这 11 名工人里选派 4 名钳工,4 名车工修理一台机床,则有多少种选派方法?“多面手”问题,确定分类讨论标准为本题的关键。
归纳总结
“多面手”问题的分类依据:按只会一种本领被选的人数来分类,将“多面手”和只会一种本领的人放在一起。虽然也能按“多面手”入选的人数和从事的任务来分类,但情况比较多,相对繁琐。
归纳总结
“多面手”问题的分类依据:按只会一种本领被选的人数来分类,将“多面手”和只会一种本领的人放在一起。虽然也能按“多面手”入选的人数和从事的任务来分类,但情况比较多,相对繁琐。
答案:
7.解:方法一:设A,B代表2名老师傅。
A,B都不在内的选派方法有C₄³·C₄⁴ = 5(种);
A,B都在内且当钳工的选派方法有C₂²C₄²C₃¹ = 10(种);
A,B都在内且当车工的选派方法有C₂²C₄³C₃¹ = 30(种);
A,B都在内,一人当钳工,一人当车工的选派方法有C₂¹A₃¹C₃¹ = 80(种);
A,B有一人在内且当钳工的选派方法有C₂¹C₄³C₃¹ = 20(种);
A,B有一人在内且当车工的选派方法有C₂¹C₄²C₃¹ = 40(种)。
故一共有5 + 10 + 30 + 80 + 20 + 40 = 185(种)选派方法。
方法二:5名男钳工有4名被选上的方法有C₅⁴C₄¹ + C₅⁴C₃¹C₄² = 75(种);
5名男钳工有3名被选上的方法有C₅³C₄² + C₅³A₃² = 100(种);
5名男钳工有2名被选上的方法有C₅²C₃² = 10(种)。
故一共有75 + 100 + 10 = 185(种)选派方法。
方法三:4名女车工都被选上的方法有C₄⁴ + C₄³C₃¹ + C₄²C₃² = 35(种);
4名女车工有3名被选上的方法有C₄³C₃¹ + C₄³A₃² = 120(种);
4名女车工有2名被选上的方法有C₄²C₃² = 30(种)。
故一共有35 + 120 + 30 = 185(种)选派方法。
A,B都不在内的选派方法有C₄³·C₄⁴ = 5(种);
A,B都在内且当钳工的选派方法有C₂²C₄²C₃¹ = 10(种);
A,B都在内且当车工的选派方法有C₂²C₄³C₃¹ = 30(种);
A,B都在内,一人当钳工,一人当车工的选派方法有C₂¹A₃¹C₃¹ = 80(种);
A,B有一人在内且当钳工的选派方法有C₂¹C₄³C₃¹ = 20(种);
A,B有一人在内且当车工的选派方法有C₂¹C₄²C₃¹ = 40(种)。
故一共有5 + 10 + 30 + 80 + 20 + 40 = 185(种)选派方法。
方法二:5名男钳工有4名被选上的方法有C₅⁴C₄¹ + C₅⁴C₃¹C₄² = 75(种);
5名男钳工有3名被选上的方法有C₅³C₄² + C₅³A₃² = 100(种);
5名男钳工有2名被选上的方法有C₅²C₃² = 10(种)。
故一共有75 + 100 + 10 = 185(种)选派方法。
方法三:4名女车工都被选上的方法有C₄⁴ + C₄³C₃¹ + C₄²C₃² = 35(种);
4名女车工有3名被选上的方法有C₄³C₃¹ + C₄³A₃² = 120(种);
4名女车工有2名被选上的方法有C₄²C₃² = 30(种)。
故一共有35 + 120 + 30 = 185(种)选派方法。
查看更多完整答案,请扫码查看


