2025年星推荐涂教材高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年星推荐涂教材高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
3. (2025·北京西城检测)某抽奖活动规则如下:从装有 3 个红球,2 个白球的袋中随机取 2 个球,每取出一个红球奖励 50 元.设一次抽奖随机取出的红球的个数为 X.
(1)求随机变量 X 的分布列,期望 $E(X)$ 和方差 $D(X)$;取 2 个球,$X = 0$,1,2.
(2)若参与一次需要花费 60 元,设每次抽奖的收益为 Y 元,写出随机变量 Y 的期望 $E(Y)$ 和方差 $D(Y)$. $Y = 50X - 60$
(1)求随机变量 X 的分布列,期望 $E(X)$ 和方差 $D(X)$;取 2 个球,$X = 0$,1,2.
(2)若参与一次需要花费 60 元,设每次抽奖的收益为 Y 元,写出随机变量 Y 的期望 $E(Y)$ 和方差 $D(Y)$. $Y = 50X - 60$
答案:
3.解:
(1)依题意,$X$的所有可能值为$0,1,2$,
$P(X = 0)=\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{5}^{2}}=\frac{1}{10},P(X = 1)=\frac{\mathrm{C}_{2}^{1}\mathrm{C}_{3}^{1}}{\mathrm{C}_{5}^{2}}=\frac{3}{5}$,
$P(X = 2)=\frac{\mathrm{C}_{3}^{2}}{\mathrm{C}_{5}^{2}}=\frac{3}{10}$,
所以$X$的分布列为
$X$ $0$ $1$ $2$
$P$ $\frac{1}{10}$ $\frac{3}{5}$ $\frac{3}{10}$
期望$E(X)=0×\frac{1}{10}+1×\frac{3}{5}+2×\frac{3}{10}=\frac{6}{5}$,
方差$D(X)=(0 - \frac{6}{5})^{2}×\frac{1}{10}+(1 - \frac{6}{5})^{2}×\frac{3}{5}+(2 - \frac{6}{5})^{2}×\frac{3}{10}=\frac{9}{25}$
(2)依题意,每次抽奖的收益$Y = 50X - 60$,
所以期望$E(Y)=50E(X)-60=50×\frac{6}{5}-60 = 0$,
方差$D(Y)=50^{2}D(X)=50^{2}×\frac{9}{25}=900$.
(1)依题意,$X$的所有可能值为$0,1,2$,
$P(X = 0)=\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{5}^{2}}=\frac{1}{10},P(X = 1)=\frac{\mathrm{C}_{2}^{1}\mathrm{C}_{3}^{1}}{\mathrm{C}_{5}^{2}}=\frac{3}{5}$,
$P(X = 2)=\frac{\mathrm{C}_{3}^{2}}{\mathrm{C}_{5}^{2}}=\frac{3}{10}$,
所以$X$的分布列为
$X$ $0$ $1$ $2$
$P$ $\frac{1}{10}$ $\frac{3}{5}$ $\frac{3}{10}$
期望$E(X)=0×\frac{1}{10}+1×\frac{3}{5}+2×\frac{3}{10}=\frac{6}{5}$,
方差$D(X)=(0 - \frac{6}{5})^{2}×\frac{1}{10}+(1 - \frac{6}{5})^{2}×\frac{3}{5}+(2 - \frac{6}{5})^{2}×\frac{3}{10}=\frac{9}{25}$
(2)依题意,每次抽奖的收益$Y = 50X - 60$,
所以期望$E(Y)=50E(X)-60=50×\frac{6}{5}-60 = 0$,
方差$D(Y)=50^{2}D(X)=50^{2}×\frac{9}{25}=900$.
4. A,B 两个投资项目的利润率分别为随机变量 $X_{1}$ 和 $X_{2}$,根据市场分析,$X_{1}$ 和 $X_{2}$ 的分布列分别为
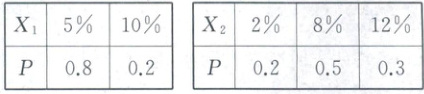
(1)在 A,B 两个项目上各投资 100 万元,$Y_{1}$(万元)和 $Y_{2}$(万元)分别表示投资项目 A 和 B 所获得的利润,求方差 $D(Y_{1})$,$D(Y_{2})$;
(2)将 $x(0\leq x\leq100)$万元投资 A 项目,$(100 - x)$万元投资 B 项目,$f(x)$表示投资 A 项目所得利润的方差与投资 B 项目所得利润的方差的和.求 $f(x)$ 的最小值,并指出 x 为何值时,$f(x)$ 取得最小值(注:$D(aX + b)=a^{2}D(X)$). 由题意写出 $f(x)$ 的解析式,再求函数的最小值.

(1)在 A,B 两个项目上各投资 100 万元,$Y_{1}$(万元)和 $Y_{2}$(万元)分别表示投资项目 A 和 B 所获得的利润,求方差 $D(Y_{1})$,$D(Y_{2})$;
(2)将 $x(0\leq x\leq100)$万元投资 A 项目,$(100 - x)$万元投资 B 项目,$f(x)$表示投资 A 项目所得利润的方差与投资 B 项目所得利润的方差的和.求 $f(x)$ 的最小值,并指出 x 为何值时,$f(x)$ 取得最小值(注:$D(aX + b)=a^{2}D(X)$). 由题意写出 $f(x)$ 的解析式,再求函数的最小值.
答案:
4.解:
(1)由题设可知$Y_1$和$Y_2$的分布列分别为
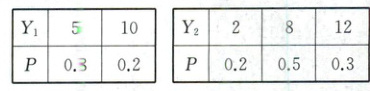
$E(Y_1)=5×0.8 + 10×0.2 = 6$,
$D(Y_1)=(5 - 6)^{2}×0.8+(10 - 6)^{2}×0.2 = 4$.
$E(Y_2)=2×0.2+8×0.5+12×0.3 = 8$,
$D(Y_2)=(2 - 8)^{2}×0.2+(8 - 8)^{2}×0.5+(12 - 8)^{2}×0.3 = 12$.
(2)$f(x)=D(\frac{x}{100}Y_1)+D(\frac{100 - x}{100}Y_2)=(\frac{x}{100})^{2}D(Y_1)+(\frac{100 - x}{100})^{2}D(Y_2)=\frac{4}{100^{2}}[x^{2}+3(100 - x)^{2}]=\frac{4}{10000}(4x^{2}-600x + 30000)=\frac{1}{625}(x - 75)^{2}+3$,
所以当$x = 75$时,$f(x)$取得最小值$3$.
4.解:
(1)由题设可知$Y_1$和$Y_2$的分布列分别为

$E(Y_1)=5×0.8 + 10×0.2 = 6$,
$D(Y_1)=(5 - 6)^{2}×0.8+(10 - 6)^{2}×0.2 = 4$.
$E(Y_2)=2×0.2+8×0.5+12×0.3 = 8$,
$D(Y_2)=(2 - 8)^{2}×0.2+(8 - 8)^{2}×0.5+(12 - 8)^{2}×0.3 = 12$.
(2)$f(x)=D(\frac{x}{100}Y_1)+D(\frac{100 - x}{100}Y_2)=(\frac{x}{100})^{2}D(Y_1)+(\frac{100 - x}{100})^{2}D(Y_2)=\frac{4}{100^{2}}[x^{2}+3(100 - x)^{2}]=\frac{4}{10000}(4x^{2}-600x + 30000)=\frac{1}{625}(x - 75)^{2}+3$,
所以当$x = 75$时,$f(x)$取得最小值$3$.
5. (2021·新高考全国卷Ⅰ)某学校组织“一带一路”知识竞赛,有 A,B 两类问题,每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A 类问题中的每个问题回答正确得 20 分,否则得 0 分;B 类问题中的每个问题回答正确得 80 分,否则得 0 分,已知小明能正确回答 A 类问题的概率为 0.8,能正确回答 B 类问题的概率为 0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答 A 类问题,记 X 为小明的累计得分,求 X 的分布列.
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
计算先回答 A 类问题的期望值 $E(X)$,再计算先回答 B 类问题的期望值,加以比较.
(1)若小明先回答 A 类问题,记 X 为小明的累计得分,求 X 的分布列.
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
计算先回答 A 类问题的期望值 $E(X)$,再计算先回答 B 类问题的期望值,加以比较.
答案:
5.解:
(1)由题可知$X$的所有可能取值为$0,20,100$.
$P(X = 0)=1 - 0.8 = 0.2$;
$P(X = 20)=0.8×(1 - 0.6)=0.32$;
$P(X = 100)=0.8×0.6 = 0.48$.
所以$X$的分布列为
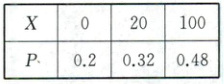
(2)由
(1)知,若小明先回答$A$类问题,则$E(X)=0×0.2+20×0.32+100×0.48 = 54.4$.
若小明先回答$B$类问题,记$Y$为小明的累计得分,则$Y$的所有可能取值为$0,80,100$.
$P(Y = 0)=1 - 0.6 = 0.4$;
$P(Y = 80)=0.6×(1 - 0.8)=0.12$;
$P(Y = 100)=0.8×0.6 = 0.48$.
所以$E(Y)=0×0.4+80×0.12+100×0.48 = 57.6$.
因为$E(Y)>E(X)$,所以小明应选择先回答$B$类问题.
5.解:
(1)由题可知$X$的所有可能取值为$0,20,100$.
$P(X = 0)=1 - 0.8 = 0.2$;
$P(X = 20)=0.8×(1 - 0.6)=0.32$;
$P(X = 100)=0.8×0.6 = 0.48$.
所以$X$的分布列为

(2)由
(1)知,若小明先回答$A$类问题,则$E(X)=0×0.2+20×0.32+100×0.48 = 54.4$.
若小明先回答$B$类问题,记$Y$为小明的累计得分,则$Y$的所有可能取值为$0,80,100$.
$P(Y = 0)=1 - 0.6 = 0.4$;
$P(Y = 80)=0.6×(1 - 0.8)=0.12$;
$P(Y = 100)=0.8×0.6 = 0.48$.
所以$E(Y)=0×0.4+80×0.12+100×0.48 = 57.6$.
因为$E(Y)>E(X)$,所以小明应选择先回答$B$类问题.
查看更多完整答案,请扫码查看


