《2025年星推荐涂教材高中数学选择性必修第三册人教版》

12. (2025·安徽阜阳模拟)重阳节是农历九月初九，二九相重，称为“重九”，又称“登高节”，由于“九九”谐音是“久久”，有长久之意，所以常在此日祭祖与推行敬老活动.某社区在重阳节开展敬老活动，已知当天参加活动的老人中女性占比为$\frac{3}{5}$，现从参加活动的老人中随机抽取14人赠送保健品，若14人中有$k$名女性的可能性最大，则$k$的值为(D)

A.8
B.7或8
C.9
D.8或9

答案： 12.D 解析：方法一：若从参加活动的老人中随机抽取14人，且
抽到的女性人数为X，则$X\sim B(14,\frac{3}{5})，$
若抽到k名女性的可能性最大，
则$\begin{cases} \mathrm{C}_{14}^{k}(\frac{3}{5})^{k}(\frac{2}{5})^{14-k}\geq\mathrm{C}_{14}^{k-1}(\frac{3}{5})^{k-1}(\frac{2}{5})^{15-k},\\ \mathrm{C}_{14}^{k}(\frac{3}{5})^{k}(\frac{2}{5})^{14-k}\geq\mathrm{C}_{14}^{k+1}(\frac{3}{5})^{k+1}(\frac{2}{5})^{13-k}, \end{cases}$
即$\begin{cases} \frac{14!}{k!(14-k)!}×\frac{3}{5}\geq\frac{14!}{(k-1)!(15-k)!}×\frac{2}{5},\\ \frac{14!}{k!(14-k)!}×\frac{2}{5}\geq\frac{14!}{(k+1)!(13-k)!}×\frac{3}{5}, \end{cases}$
解得$8\leq k\leq9，$
又$k\in N^*，$故k=8或9.
方法二：$(n+1)p=15×\frac{3}{5}=9，$所以当k=8或9时可能性
最大.

13. (多选题)(2025·安徽黄山模拟)为了防止受到核污染的产品影响民众的身体健康，要求产品在进入市场前必须进行两轮核辐射检测，只有两轮都合格才能进行销售，否则不能销售.已知某产品第一轮检测不合格的概率为$\frac{1}{6}$，第二轮检测不合格的概率为$\frac{1}{10}$，两轮检测是否合格相互没有影响.若产品可以销售，则每件产品获利40元；若产品不能销售，则每件产品亏损80元.已知一箱中有4件产品，记一箱产品获利$X$元，则下列说法正确的是(ABD)

A.该产品能销售的概率为$\frac{3}{4}$
B.若$\xi$表示一箱产品中可以销售的件数，则$\xi\sim B(4,\frac{3}{4})$
C.若$\xi$表示一箱产品中可以销售的件数，则$P(X = 40)=P(\xi = 3)=\frac{7}{120}$
D.$P(X = - 80)=\frac{27}{128}$

答案： 13.ABD 解析：选项A，该产品能销售的概率为$(1-\frac{1}{6})×$
$(1-\frac{1}{10})=\frac{3}{4}，$故选项A正确；
选项B，由A可得每件产品能销售的概率为$\frac{3}{4}，$一箱中有
4件产品，记一箱产品中可以销售的件数为$\xi，$则$\xi\sim B(4,\frac{3}{4})，$
故选项B正确；
选项C，由题意得$P(\xi=3)=\mathrm{C}_{4}^{3}×(\frac{3}{4})^{3}×\frac{1}{4}=\frac{27}{64}，$当$\xi=3$时，
X=3×40-1×80=40(元)，所以$P(X=40)=P(\xi=3)$
$=\frac{27}{64}，$
故选项C不正确；
选项D，由题意得X=-80，即4件产品中有2件能销售，有
2件不能销售，
所以$P(X=-80)=\mathrm{C}_{4}^{2}×(\frac{3}{4})^{2}×(\frac{1}{4})^{2}=\frac{27}{128}，$故选项D
正确.

14. (多选题)(2025·山东临沂模拟)为了增强学生的冬奥会知识，弘扬奥林匹克精神，某市多所中小学开展了冬奥会项目科普活动.为了了解学生对冰壶这个项目的了解情况，在该市中小学中随机抽取了10所学校，10所学校中了解这个项目的人数如图所示.

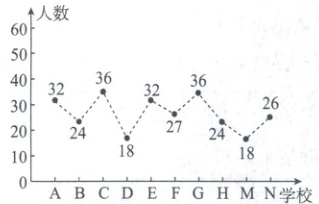
若从这10所学校中随机选取2所学校进行这个项目的科普活动，记$X$为被选中的学校中了解冰壶的人数在30以上的学校个数，则(BC)

A.$X$的取值范围为$\{0,1,2,3\}$
B.$P(X = 0)=\frac{1}{3}$
C.$P(X = 1)=\frac{8}{15}$
D.$E(X)=\frac{3}{5}$

答案： 14.BC 解析：X的取值范围为{0,1,2}，了解冰壶的人数在30以
上的学校有4所，$P(X=0)=\frac{\mathrm{C}_{6}^{0}\mathrm{C}_{4}^{2}}{\mathrm{C}_{10}^{2}}=\frac{1}{3}，$
$P(X=1)=\frac{\mathrm{C}_{6}^{1}\mathrm{C}_{4}^{1}}{\mathrm{C}_{10}^{2}}=\frac{8}{15}，$$P(X=2)=\frac{\mathrm{C}_{6}^{2}\mathrm{C}_{4}^{0}}{\mathrm{C}_{10}^{2}}=\frac{2}{15}，$
所以$E(X)=0×\frac{1}{3}+1×\frac{8}{15}+2×\frac{2}{15}=\frac{4}{5}.$

15. (2025·上海普陀模拟)某区为推进教育数字化转型，通过聚合区域学校的教育资源，依托AI技术搭建了区域智慧题库系统，形成了“A通识过关—B综合拓展—C创新提升”三层动态原库，且A，B，C三层题量之比为7：3：2，设该题库中任意1道题被选到的可能性都相同.
(1)现有4人参加一项比赛，若每人分别独立地从该题库中随机选取一道题作答，求这4人中至少有2人的选题来自B层的概率；
(2)现采用分层随机抽样的方法，使用智能组卷系统从该题库中选取12道题生成试卷，若某老师要从生成的这份12道题的试卷中随机选取3道题做进一步改编，记该老师选到A层题的题数为$X$，求$X$的分布列与期望$E(X)$.

答案： 15.解：
(1)因为A,B,C三层题量之比为7:3:2，
所以在B层选题的概率为$\frac{3}{12}=\frac{1}{4}，$不在B层选题的概率为
$1-\frac{1}{4}=\frac{3}{4}.$
设至少2人的选题来自B层的概率为P，从B层选题数量
为$X_1，$
由题意得$X_1\sim B(4,\frac{1}{4})，$而二项分布概率公式为$P(X_1=$
$k)=\mathrm{C}_{4}^{k}(\frac{1}{4})^{k}(\frac{3}{4})^{4-k}，$
则至少2人的选题来自B层的概率为$P=P(X_1=2)+$
$P(X_1=3)+P(X_1=4)，$
故$P=\mathrm{C}_{4}^{2}(\frac{1}{4})^{2}(\frac{3}{4})^{2}+\mathrm{C}_{4}^{3}(\frac{1}{4})^{3}(\frac{3}{4})^{1}+\mathrm{C}_{4}^{4}(\frac{1}{4})^{4}=\frac{54}{256}+$
$\frac{12}{256}+\frac{1}{256}=\frac{67}{256}.$
(2)因为A,B,C三层题量之比为7:3:2，
所以在A层抽到7道，且X可取0,1,2,3，
则$P(X=0)=\frac{\mathrm{C}_{3}^{0}\mathrm{C}_{9}^{3}}{\mathrm{C}_{12}^{3}}=\frac{1}{22}，$$P(X=1)=\frac{\mathrm{C}_{3}^{1}\mathrm{C}_{9}^{2}}{\mathrm{C}_{12}^{3}}=\frac{7}{22}，$
$P(X=2)=\frac{\mathrm{C}_{3}^{2}\mathrm{C}_{9}^{1}}{\mathrm{C}_{12}^{3}}=\frac{21}{44}，$$P(X=3)=\frac{\mathrm{C}_{3}^{3}\mathrm{C}_{9}^{0}}{\mathrm{C}_{12}^{3}}=\frac{7}{44}.$
其分布列为
X 0 1 2 3
$P \frac{1}{22} \frac{7}{22} \frac{21}{44} \frac{7}{44}$
所以期望$E(X)=0×\frac{1}{22}+1×\frac{7}{22}+2×\frac{21}{44}+3×\frac{7}{44}=\frac{7}{4}.$