《2025年星推荐涂教材高中数学选择性必修第三册人教版》

9. (2025·山东济南模拟)最近，李师傅一家三口就如何将手中的$10$万元进行投资理财提出了三种方案：
方案一，李师傅的儿子认为：根据股市收益大的特点，应该将$10$万元全部用来买股票.据分析预测，投资股市一年后可能获利$40\%$，也可能亏损$20\%$（只有这两种可能），且获利的概率为$\frac{1}{2}$.
方案二，李师傅认为：现在股市风险大，基金风险较小，应该将$10$万元全部用来买基金.据分析预测，投资基金一年后可能获利$20\%$，可能损失$10\%$，也可能不赔不赚，且这三种情况发生的概率分别为$\frac{3}{5}$，$\frac{1}{5}$，$\frac{1}{5}$.
方案三，李师傅的妻子认为：投资股市、基金均有风险，应该将$10$万元全部存入银行一年，现在存款年利率为$4\%$.
针对以上三种投资方案，请你为李师傅家选择一种合理的理财方案，并说明理由.

答案： 9.解：若按方案一执行，设收益为$\xi$万元，则其分布列为 $\xi$ $4$ $-2$ $P$ $\frac{1}{2}$ $\frac{1}{2}$ 所以$E(\xi)=4×\frac{1}{2}+(-2)×\frac{1}{2}=1$. 若按方案二执行，设收益为$\eta$万元，则其分布列为 $\eta$ $2$ $0$ $-1$ $P$ $\frac{3}{5}$ $\frac{1}{5}$ $\frac{1}{5}$ 所以$E(\eta)=2×\frac{3}{5}+0×\frac{1}{5}+(-1)×\frac{1}{5}=1$. 若按方案三执行，收益$y = 10×4\% = 0.4$（万元）. 因为$E(\xi)=E(\eta)＞y$，所以应从方案一、方案二中选择一种 投资方案. 由$D(\xi)=(4 - 1)^2×\frac{1}{2}+(-2 - 1)^2×\frac{1}{2}=9$， $D(\eta)=(2 - 1)^2×\frac{3}{5}+(0 - 1)^2×\frac{1}{5}+(-1 - 1)^2×\frac{1}{5}=\frac{8}{5}$. 易知$D(\xi)＞D(\eta)$.这说明虽然方案一、方案二的期望收益相 等，但方案二更稳定，所以建议李师傅家选择方案二.

10. (2025·浙江宁波模拟)甲、乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完$5$局仍未出现连胜，则判定获胜局数多者赢得比赛，假设每局甲获胜的概率为$\frac{2}{3}$，乙获胜的概率为$\frac{1}{3}$，各局比赛结果相互独立.记$X$为比赛决出胜负时的总局数，则$X$的均值(数学期望)为(A)

A.$\frac{224}{81}$
B.$\frac{34}{9}$
C.$\frac{24}{9}$
D.$\frac{304}{81}$

答案： 10.A 解析：设$A_k$表示“第$k$局甲获胜”，$B_k$表示“第$k$局乙获 胜”，则$P(A_k)=\frac{2}{3}$，$P(B_k)=\frac{1}{3}$，$k = 1,2,3,4,5$. 由题意，$X$的所有可能的值为$2$，$3$，$4$，$5$，则 $P(X = 2)=P(A_1A_2)+P(B_1B_2)$ $=P(A_1)P(A_2)+P(B_1)P(B_2)=\frac{5}{9}$， $P(X = 3)=P(B_1A_2A_3)+P(A_1B_2B_3)$ $=P(B_1)P(A_2)P(A_3)+P(A_1)P(B_2)P(B_3)=\frac{2}{9}$， $P(X = 4)=P(A_1B_2A_3A_4)+P(B_1A_2B_3B_4)$ $=P(A_1)P(B_2)P(A_3)P(A_4)+P(B_1)P(A_2)P(B_3)·$ $P(B_4)=\frac{10}{81}$， $P(X = 5)=1 - P(X = 2)-P(X = 3)-P(X = 4)=\frac{8}{81}$. 故$X$的分布列为 $X$ $2$ $3$ $4$ $5$ $P$ $\frac{5}{9}$ $\frac{2}{9}$ $\frac{10}{81}$ $\frac{8}{81}$ 则$E(X)=2×\frac{5}{9}+3×\frac{2}{9}+4×\frac{10}{81}+5×\frac{8}{81}=\frac{224}{81}$.

11. (多选题)(2025·山东烟台质检)某学校共有$6$个学生餐厅，甲、乙、丙、丁四位同学每人随机地选择一家餐厅就餐(选择每个餐厅的概率相同)，则下列结论正确的有(ACD)

A.四人去了四个不同餐厅就餐的概率为$\frac{5}{18}$
B.四人去了同一家餐厅就餐的概率为$\frac{1}{1296}$
C.四人中恰有两人去了第一餐厅就餐的概率为$\frac{25}{216}$
D.四人中去第一餐厅就餐的人数的均值为$\frac{2}{3}$

答案： 11.ACD 解析：四人去餐厅就餐的情况共有$6^4$种，其中四人去 了四个不同餐厅就餐的情况有$A_{6}^{4}$种，则四人去了四个不同 餐厅就餐的概率为$\frac{A_{6}^{4}}{6^{4}}=\frac{5}{18}$，故A正确；同理，四人去了同一家餐厅就餐的概率为$\frac{6}{6^{4}}=\frac{1}{216}$，故B错误；四人中恰有两人 去了第一餐厅就餐的概率为$\frac{C_{4}^{2}×5^{2}}{6^{4}}=\frac{25}{216}$，故C正确；设四 人中去第一餐厅就餐的人数为$\xi$，则$\xi = 0$，$1$，$2$，$3$，$4$，则$P(\xi=$ $0)=\frac{5^{4}}{6^{4}}$，$P(\xi = 1)=\frac{C_{4}^{1}×5^{3}}{6^{4}}$，$P(\xi = 2)=\frac{C_{4}^{2}×5^{2}}{6^{4}}$，$P(\xi = 3)=\frac{C_{4}^{3}×5}{6^{4}}$，$P(\xi = 4)=\frac{1}{6^{4}}$，则四人中去第一餐厅就餐的人数的均值$E(\xi)=0×\frac{5^{4}}{6^{4}}+1×$ $\frac{C_{4}^{1}×5^{3}}{6^{4}}+2×\frac{C_{4}^{2}×5^{2}}{6^{4}}+3×\frac{C_{4}^{3}×5}{6^{4}}+4×\frac{1}{6^{4}}=\frac{2}{3}$，故D正确.

12. (2025·山东青岛模拟)某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历，假定该毕业生得到甲公司面试机会的概率为$\frac{2}{3}$，得到乙、丙两个公司面试机会的概率均为$p$，且三个公司是否让其面试是相互独立的.设$X$为该毕业生得到面试机会的公司个数.若$P(X = 0) = \frac{1}{12}$，则$D(X)=$$\frac{13}{18}$.

答案： 12.$\frac{13}{18}$ 解析：由$P(X = 0)=\frac{1}{12}$知，$\frac{1}{3}×(1 - p)^2=\frac{1}{12}$，$0＜p＜$ $1$，得$p=\frac{1}{2}$.由题意知$X$为该毕业生得到面试机会的公司 个数，则$X$的所有可能取值是$0$，$1$，$2$，$3$， $P(X = 1)=\frac{2}{3}×(1 - \frac{1}{2})^2+\frac{1}{3}×\frac{1}{2}×(1 - \frac{1}{2})+(1 -$ $\frac{1}{2})×\frac{1}{2}×\frac{1}{3}$， $P(X = 2)=\frac{2}{3}×\frac{1}{2}×(1 - \frac{1}{2})+\frac{2}{3}×(1 - \frac{1}{2})×\frac{1}{2}+$ $\frac{1}{3}×\frac{1}{2}×\frac{1}{2}=\frac{5}{12}$， $P(X = 3)=\frac{2}{3}×(\frac{1}{2})^2=\frac{1}{6}$， 所以$E(X)=0×\frac{1}{12}+1×\frac{1}{3}+2×\frac{5}{12}+3×\frac{1}{6}=\frac{5}{3}$， 所以$D(X)=\frac{1}{12}×(0 - \frac{5}{3})^2+\frac{1}{3}×(1 - \frac{5}{3})^2+\frac{5}{12}×(2 -$ $\frac{5}{3})^2+\frac{1}{6}×(3 - \frac{5}{3})^2=\frac{13}{18}$.

13. (2025·全国卷Ⅰ)一个箱子里有$5$个相同的球，分别以$1 \sim 5$标号，若每次取一个，有放回地取三次，记至少取出一次的球的个数为$X$，则数学期望$E(X)=$$\frac{61}{25}$.

答案： 13.$\frac{61}{25}$ 解析：依题意，$X$的可能取值为$1$，$2$，$3$，总的选取可能数 为$5^3 = 125$， 其中$X = 1$表示三次抽取同一个球，选择球的编号有$5$种方 式，故$P(X = 1)=\frac{5}{125}=\frac{1}{25}$， $X = 2$表示恰好两种不同的球被取出（即一球出现两次，另一 球出现一次）， 选取出现两次的球有$5$种方式，选取出现一次的球有$4$种方 式，其中选取出现一次的球的位置有$3$种可能，故事件$X = 2$ 的可能情况有$5×4×3 = 60$（种）， 故$P(X = 2)=\frac{60}{125}=\frac{12}{25}$， $X = 3$表示三种不同的球被取出， 由排列数可知事件$X = 3$的可能情况有$5×4×3 = 60$（种）， 故$P(X = 3)=\frac{60}{125}=\frac{12}{25}$， 所以$E(X)=1× P(X = 1)+2× P(X = 2)+3× P(X = 3)$ $=1×\frac{1}{25}+2×\frac{12}{25}+3×\frac{12}{25}=\frac{61}{25}$.

14. 某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕，基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质，基地收益如下表所示：

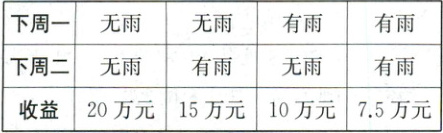
若基地额外聘请工人，可在下周一当天完成全部采摘任务.无雨时，收益为$20$万元；有雨时，收益为$10$万元，额外聘请工人的成本为$a$万元.
已知下周一和下周二有雨的概率相同，两天是否下雨互不影响，基地收益为$20$万元的概率为$0.36$.
(1)若不额外聘请工人，写出基地收益$X$（万元）的分布列及基地的预期收益.
(2)该基地是否应该额外聘请工人？请说明理由.

答案： 14.解：
(1)设下周一无雨的概率为$p$，由题意，得$p^2 = 0.36$，所以 $p = 0.6$. 基地收益$X$的所有可能取值为$20$，$15$，$10$，$7.5$， 则$P(X = 20)=0.36$，$P(X = 15)=0.24$，  $P(X = 7.5)=0.16$. 所以基地收益$X$的分布列为 $X$ $20$ $15$ $10$ $7.5$ $P$ $0.36$ $0.24$ $0.24$ $0.16$ $E(X)=20×0.36 + 15×0.24 + 10×0.24 + 7.5×0.16 = 14.4$， 所以基地的预期收益为$14.4$万元.\n
(2)设基地额外聘请工人时的收益为$Y$万元， 此时预期收益$E(Y)=20×0.6 + 10×0.4 - a = 16 - a$， $E(Y)-E(X)=1.6 - a$. 综上，当额外聘请工人的成本高于$1.6$万元时，不额外聘请 工人；成本低于$1.6$万元时，则额外聘请工人；成本恰为 $1.6$万元时，可额外聘请工人，也可不额外聘请工人.