《2025年星推荐涂教材高中数学选择性必修第三册人教版》

8. (2025·山东潍坊检测)课外活动小组共 13 人，其中男生 8 人，女生 5 人，并且男、女生各有一名队长，现从中选 5 人主持某项活动，依下列条件各有多少种选法？
(1)至少有一名队长当选；间接法
(2)至多有两名女生当选；三类：含女生 0 名；1 名；2 名。
(3)既要有队长，又要有女生当选。分两类：女队长当选；女队长没当选。
解题通法
“至多”“至少”问题的常用解题方法
(1)直接分类法，但要注意分类要细要全。
(2)间接法，注意找准对立面，确保不重不漏。

答案： 8.解:
(1)C₁₃⁵ - C₁₁³ = 825(种)。
(2)至多有2名女生当选含有三类:有2名女生当选；只有1名女生当选；没有女生当选，所以共有C₅²C₈³ + C₅¹C₈⁴ + C₈⁵ = 966(种)选法。
(3)分两类:第一类:女队长当选，有C₁₂⁴ = 495(种)选法；第二类:女队长没当选，有C₄¹C₇³ + C₄²C₇² + C₄³C₇¹ + C₄⁴ = 295(种)选法，所以共有495 + 295 = 790(种)选法。

9. (2025·河北邯郸模拟)平面直角坐标系内的一个质点从原点出发，每次向右或向上移动 1 个单位长度，则移动 8 次后，质点恰好位于点 $ (4,4) $ 的移动方式有由 $ (0,0) \to (4,4) $。(B)

A.56 种
B.70 种
C.210 种
D.1680 种

答案： 9.B解析:由题可知，质点在这8次移动过程中，一共向右移动了4个单位长度，向上移动了4个单位长度，所以共有C₈⁴ = 70(种)移动方式。

10. (2025·四川眉山月考)如果一个凸多面体是 $ n $ 棱锥，那么这个凸多面体的所有顶点所确定的直线共有$\frac{n(n + 1)}{2}$条。这些直线中共有 $ f(n) $ 对异面直线，则 $ f(4) = $12，$ f(n) = $$\frac{n(n - 1)(n - 2)}{2}$(用数字或含 $ n $ 的代数式表示)。表示四棱锥中异面直线的对数。
归纳总结
1. 解几何图形中的组合应用题的思路：(1)利用定义、性质分析其几何特征；(2)合理构建完成事件的方式和方法，或分步、分类，或构造模型。
2. 解几何图形中的组合问题的常用方法：(1)直接法；(2)间接法；(3)构造模型法。

答案：
10.$\frac{n(n + 1)}{2}$ 12 $\frac{n(n - 1)(n - 2)}{2}$ 解析:n棱锥共(n + 1)个顶点，依两点确定一条直线，有Cₙ₊₁² = $\frac{n(n + 1)}{2}$条直线。f
(4)表示四棱锥中的异面直线的对数，如图，每条侧棱和底面上不共顶点的两条底边、一条对角线共形成3对异面直线，即f
(4) = 4×3 = 12。
　　　　　　　　
同理，一条侧棱与底面上(n - 2)条底边异面，又与Cₙ₋₁² - (n - 1) + 1条底面对角线异面，即与这条侧棱异面的直线有Cₙ₋₁² - (n - 1) + 1 + (n - 2) = Cₙ₋₁² = $\frac{(n - 1)(n - 2)}{2}$条，故n条侧棱形成的异面直线的对数为f(n) = $\frac{n(n - 1)(n - 2)}{2}$。

11. 某城市一条道路上有 12 盏路灯，为了节约用电而不影响正常的照明，可以熄灭其中的 3 盏，但两端路灯不能熄灭，也不能熄灭相邻的 2 盏，那么熄灯方法共有56种。(用数字作答)
学习笔记
排列、组合应用题的背景丰富、千姿百态、情景陌生、无特定的模式和规律可循，因此必须认真审题，把握问题的本质特征，化归为排列、组合的常规模型进而求解。

答案： 11.56解析:“亮灯”“灭灯”元素之间互异，可视为互异的元素，不考虑顺序，属于组合问题。“灭灯”不相邻，应采取“插空法”分两步完成:第一步，安排9盏亮灯，因为亮灯相同，只是位置不同，共有C₉⁹种；第二步，将3盏熄灭的灯插到8个空里，有C₈³种。根据分步乘法计数原理，共有C₉⁹·C₈³ = 56(种)熄灯方法。

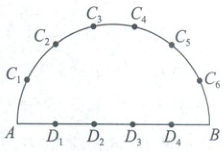
12. (2025·山东济南检测)如图，在以 $ AB $ 为直径的半圆周上，有异于 $ A $，$ B $ 的六个点 $ C_{1} $，$ C_{2} $，$ C_{3} $，$ C_{4} $，$ C_{5} $，$ C_{6} $，直径 $ AB $ 上有异于 $ A $，$ B $ 的四个点 $ D_{1} $，$ D_{2} $，$ D_{3} $，$ D_{4} $。
(1)以这 10 个点中的 3 个点为顶点作三角形可作出多少个？其中含点 $ C_{1} $ 的有多少个？
(2)以图中的 12 个点(包括 $ A $，$ B $)中的 4 个点为顶点，可作出多少个四边形？
分类：

①“$ C $系列”点中任取 4 个；
②“$ C $系列”点中取 3 个，“$ D $系列”点中取 1 个；
③“$ C $系列”点和“$ D $系列”点中各取 2 个。

答案： 12.解:
(1)可分三种情况处理:①在C₁,C₂,…,C₆这六个点中任取三点构成一个三角形，有C₆³个；②在C₁,C₂,…,C₆这六个点中任取两点，D₁,D₂,D₃,D₄这四个点中任取一点构成一个三角形，有C₆²C₄¹个；③在C₁,C₂,…,C₆这六个点中任取一点，D₁,D₂,D₃,D₄这四个点中任取两点构成一个三角形，有C₆¹C₄²个。所以共可以作出C₆³ + C₆²C₄¹ + C₆¹C₄² = 116(个)三角形，其中含点C₁的三角形有C₅² = 36(个)。
(2)构成一个四边形，需要四个点，且无三点共线，因此可分三种情况处理:①在C₁,C₂,…,C₆这六个点中任取四点构成一个四边形，有C₆⁴个；②在C₁,C₂,…,C₆这六个点中任取三点，D₁,D₂,D₃,D₄，A，B这六个点中任取一点构成一个四边形，有C₆³C₆¹个；③在C₁,C₂,…,C₆这六个点中任取两点，D₁,D₂,D₃,D₄，A，B这六个点中任取两点构成一个四边形，有C₆²C₆²个。所以共可以作出C₆⁴ + C₆³C₆¹ + C₆²C₆² = 360(个)四边形。

13. (1)(浙江卷)从 1，3，5，7，9 中任取 2 个数字，从 0，2，4，6 中任取 2 个数字，一共可以组成个没有重复数字的四位数。(用数字作答)
(2)(2025·山东泰安一模)从 5 名同学中选择 4 人参加三天志愿服务活动，有一天安排两人，另两天各安排一人，共有种安排方法。(用数字作答)

答案： 13.
(1)1260
(2)180解析:
(1)若取的4个数字不包括0，则可以组成的四位数的个数为C₉⁴A₄⁴；若取的4个数字包括0，则可以组成的四位数的个数为C₉³C₃¹A₃³。综上，一共可以组成的没有重复数字的四位数的个数为C₉⁴A₄⁴ + C₉³C₃¹A₃³ = 720 + 540 = 1260。
(2)第一步，从5人中选4人，共有C₅⁴ = 5(种)取法；第二步，将4人分成三组，共有C₄² = 6(种)分法，再进行全排，有A₃³ = 6(种)排法。
由分步乘法计数原理知，共有C₅⁴C₄²A₃³ = 5×6×6 = 180(种)安排方法。