第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
7. 已知数据 $x_1$,$x_2$,$x_3$ 的平均数是 $10$,请你根据算术平均数的知识解决以下问题:
(1) 数据 $x_1 + 1$,$x_2 + 2$,$x_3 + 3$ 的平均数为
(2) 数据 $2x_1$,$2x_2$,$2x_3$ 的平均数为
(3) 数据 $\frac{x_1}{3}$,$\frac{x_2}{3}$,$\frac{x_3}{3}$ 的平均数为
(4) 求数据 $ax_1 + b$,$ax_2 + b$,$ax_3 + b$ 的平均数,写出解题过程.
(1) 数据 $x_1 + 1$,$x_2 + 2$,$x_3 + 3$ 的平均数为
12
.(2) 数据 $2x_1$,$2x_2$,$2x_3$ 的平均数为
20
.(3) 数据 $\frac{x_1}{3}$,$\frac{x_2}{3}$,$\frac{x_3}{3}$ 的平均数为
$\frac{10}{3}$
.(4) 求数据 $ax_1 + b$,$ax_2 + b$,$ax_3 + b$ 的平均数,写出解题过程.
答案:
1. (1)
已知$\frac{x_{1}+x_{2}+x_{3}}{3}=10$,即$x_{1}+x_{2}+x_{3}=30$。
对于数据$x_{1}+1,x_{2}+2,x_{3}+3$,其平均数为$\frac{(x_{1}+1)+(x_{2}+2)+(x_{3}+3)}{3}$。
展开式子得$\frac{x_{1}+x_{2}+x_{3}+1 + 2+3}{3}$,把$x_{1}+x_{2}+x_{3}=30$代入,得$\frac{30 + 6}{3}=12$。
2. (2)
对于数据$2x_{1},2x_{2},2x_{3}$,其平均数为$\frac{2x_{1}+2x_{2}+2x_{3}}{3}$。
提取公因式$2$得$2×\frac{x_{1}+x_{2}+x_{3}}{3}$,把$\frac{x_{1}+x_{2}+x_{3}}{3}=10$代入,得$2×10 = 20$。
3. (3)
对于数据$\frac{x_{1}}{3},\frac{x_{2}}{3},\frac{x_{3}}{3}$,其平均数为$\frac{\frac{x_{1}}{3}+\frac{x_{2}}{3}+\frac{x_{3}}{3}}{3}$。
提取公因式$\frac{1}{3}$得$\frac{1}{3}×\frac{x_{1}+x_{2}+x_{3}}{3}$,把$\frac{x_{1}+x_{2}+x_{3}}{3}=10$代入,得$\frac{10}{3}$。
4. (4)
解:对于数据$ax_{1}+b,ax_{2}+b,ax_{3}+b$,其平均数为$\frac{(ax_{1}+b)+(ax_{2}+b)+(ax_{3}+b)}{3}$。
展开式子得$\frac{ax_{1}+ax_{2}+ax_{3}+3b}{3}$。
提取公因式$a$得$\frac{a(x_{1}+x_{2}+x_{3})+3b}{3}$。
因为$\frac{x_{1}+x_{2}+x_{3}}{3}=10$,即$x_{1}+x_{2}+x_{3}=30$,代入上式得$\frac{30a + 3b}{3}=10a + b$。
综上,(1)答案为$12$;(2)答案为$20$;(3)答案为$\frac{10}{3}$;(4)平均数为$10a + b$。
已知$\frac{x_{1}+x_{2}+x_{3}}{3}=10$,即$x_{1}+x_{2}+x_{3}=30$。
对于数据$x_{1}+1,x_{2}+2,x_{3}+3$,其平均数为$\frac{(x_{1}+1)+(x_{2}+2)+(x_{3}+3)}{3}$。
展开式子得$\frac{x_{1}+x_{2}+x_{3}+1 + 2+3}{3}$,把$x_{1}+x_{2}+x_{3}=30$代入,得$\frac{30 + 6}{3}=12$。
2. (2)
对于数据$2x_{1},2x_{2},2x_{3}$,其平均数为$\frac{2x_{1}+2x_{2}+2x_{3}}{3}$。
提取公因式$2$得$2×\frac{x_{1}+x_{2}+x_{3}}{3}$,把$\frac{x_{1}+x_{2}+x_{3}}{3}=10$代入,得$2×10 = 20$。
3. (3)
对于数据$\frac{x_{1}}{3},\frac{x_{2}}{3},\frac{x_{3}}{3}$,其平均数为$\frac{\frac{x_{1}}{3}+\frac{x_{2}}{3}+\frac{x_{3}}{3}}{3}$。
提取公因式$\frac{1}{3}$得$\frac{1}{3}×\frac{x_{1}+x_{2}+x_{3}}{3}$,把$\frac{x_{1}+x_{2}+x_{3}}{3}=10$代入,得$\frac{10}{3}$。
4. (4)
解:对于数据$ax_{1}+b,ax_{2}+b,ax_{3}+b$,其平均数为$\frac{(ax_{1}+b)+(ax_{2}+b)+(ax_{3}+b)}{3}$。
展开式子得$\frac{ax_{1}+ax_{2}+ax_{3}+3b}{3}$。
提取公因式$a$得$\frac{a(x_{1}+x_{2}+x_{3})+3b}{3}$。
因为$\frac{x_{1}+x_{2}+x_{3}}{3}=10$,即$x_{1}+x_{2}+x_{3}=30$,代入上式得$\frac{30a + 3b}{3}=10a + b$。
综上,(1)答案为$12$;(2)答案为$20$;(3)答案为$\frac{10}{3}$;(4)平均数为$10a + b$。
1. 填空题。
(1)某大学自主招生考试只考数学和物理.计算综合得分时,按数学占$60\%$,物理占$40\%$计算.已知孔明数学得分为$95$分,综合得分为$93$分,那么孔明物理得分是
(2)如图所示是某班$20$人在“献爱心”活动中捐书的情况,该班人均捐书

(3)某次能力测试中,$10$人的成绩统计如下表,则这$10$人成绩的平均数为

(4)某校规定:学生期末总评成绩由卷面成绩、研究性学习成绩、平日成绩三部分构成,各部分所占比例如图所示.小明本学期数学学科三部分的成绩分别是$90$分、$80$分、$85$分,则小明的数学期末总评成绩为

(5)某市广播电视局欲招聘播音员一名,对甲、乙两名候选人进行了两项素质测试,两人的两项测试成绩如下表:
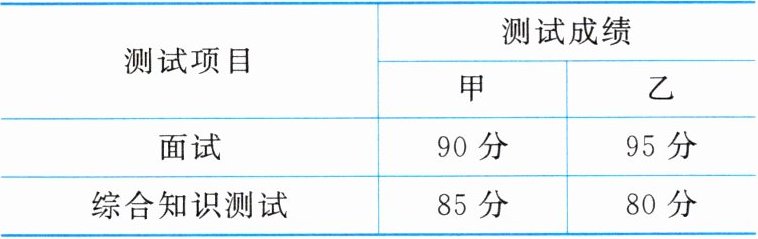
根据实际需要,广播电视局将面试、综合知识测试的得分按$3:2$的比例计算两人的总成绩,那么
(1)某大学自主招生考试只考数学和物理.计算综合得分时,按数学占$60\%$,物理占$40\%$计算.已知孔明数学得分为$95$分,综合得分为$93$分,那么孔明物理得分是
90
分.(2)如图所示是某班$20$人在“献爱心”活动中捐书的情况,该班人均捐书
2.8
本.
(3)某次能力测试中,$10$人的成绩统计如下表,则这$10$人成绩的平均数为
3.1分
.
(4)某校规定:学生期末总评成绩由卷面成绩、研究性学习成绩、平日成绩三部分构成,各部分所占比例如图所示.小明本学期数学学科三部分的成绩分别是$90$分、$80$分、$85$分,则小明的数学期末总评成绩为
87
分.
(5)某市广播电视局欲招聘播音员一名,对甲、乙两名候选人进行了两项素质测试,两人的两项测试成绩如下表:

根据实际需要,广播电视局将面试、综合知识测试的得分按$3:2$的比例计算两人的总成绩,那么
乙
将被录用.(填“甲”或“乙”)
答案:
1.
(1)90
(2)2.8
(3)3.1分
(4)87
(5)乙
(1)90
(2)2.8
(3)3.1分
(4)87
(5)乙
查看更多完整答案,请扫码查看


