第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
2. 选择题。
(1) 教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛。两人在相同条件下各打了 5 发子弹,命中环数如下:
甲:9 8 7 7 9
乙:10 8 9 7 6
那么教练选择的是(
A. 甲
B. 乙
C. 甲、乙都可以
D. 无法确定
(2) 某班一学习小组 6 名学生的体育成绩如下表,则这组学生体育成绩的众数、中位数和方差依次为(

A. 28 分,28 分,1 分$ ^2 $
B. 28 分,27.5 分,1 分$ ^2 $
C. 3 分,2.5 分,5 分$ ^2 $
D. 3 分,2 分,5 分$ ^2 $
(3) 一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖):

那么被遮盖的两个数据依次是(
A. 80,2
B. 80,$ \sqrt{2} $
C. 78,2
D. 78,$ \sqrt{2} $
(4) 在踢毽比赛人选选拔中,根据小立和小明每分钟踢毽的成绩制作了如下统计表,则下列判断中正确的有(
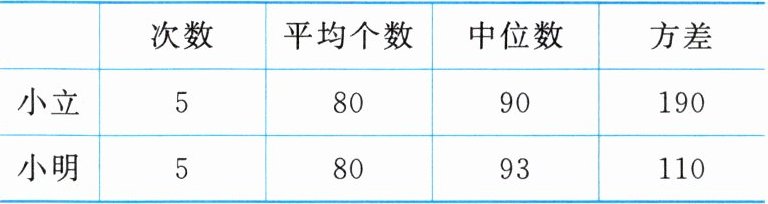
① 小立的平均成绩高于小明的平均成绩;
② 小立的成绩的波动比小明的大;
③ 选择小明参加比赛。
A. 1 个
B. 2 个
C. 3 个
D. 都不正确
(1) 教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛。两人在相同条件下各打了 5 发子弹,命中环数如下:
甲:9 8 7 7 9
乙:10 8 9 7 6
那么教练选择的是(
A
)A. 甲
B. 乙
C. 甲、乙都可以
D. 无法确定
(2) 某班一学习小组 6 名学生的体育成绩如下表,则这组学生体育成绩的众数、中位数和方差依次为(
A
)
A. 28 分,28 分,1 分$ ^2 $
B. 28 分,27.5 分,1 分$ ^2 $
C. 3 分,2.5 分,5 分$ ^2 $
D. 3 分,2 分,5 分$ ^2 $
(3) 一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖):

那么被遮盖的两个数据依次是(
C
)A. 80,2
B. 80,$ \sqrt{2} $
C. 78,2
D. 78,$ \sqrt{2} $
(4) 在踢毽比赛人选选拔中,根据小立和小明每分钟踢毽的成绩制作了如下统计表,则下列判断中正确的有(
B
)
① 小立的平均成绩高于小明的平均成绩;
② 小立的成绩的波动比小明的大;
③ 选择小明参加比赛。
A. 1 个
B. 2 个
C. 3 个
D. 都不正确
答案:
2.
(1)A
(2)A
(3)C
(4)B
(1)A
(2)A
(3)C
(4)B
3. 九年级(二)班组织了一次朗读比赛,甲、乙两队各 10 人的比赛成绩(单位:分)如下表:

(1) 甲队成绩的中位数是
(2) 计算乙队成绩的平均数和方差。
(3) 已知甲队成绩的方差是 1.4 分$ ^2 $,则成绩较为整齐的是

(1) 甲队成绩的中位数是
9.5
分,乙队成绩的众数是10
分。(2) 计算乙队成绩的平均数和方差。
乙队的平均成绩是$\frac {1}{10}×(10×4+8×2+7+9×3)=9$(分),方差是$\frac {1}{10}×[4×(10-9)^{2}+2×(8-9)^{2}+(7-9)^{2}+3×(9-9)^{2}]=1$(分²).
(3) 已知甲队成绩的方差是 1.4 分$ ^2 $,则成绩较为整齐的是
乙
队。
答案:
3.解:
(1)9.5,10
(2)乙队的平均成绩是$\frac {1}{10}×(10×4+8×2+7+9×3)=9$(分),方差是$\frac {1}{10}×[4×(10-9)^{2}+2×(8-9)^{2}+(7-9)^{2}+3×(9-9)^{2}]=1$(分²).
(3)
∵甲队成绩的方差是1.4分²,乙队成绩的方差是1分²,
∴成绩较为整齐的是乙队.
(1)9.5,10
(2)乙队的平均成绩是$\frac {1}{10}×(10×4+8×2+7+9×3)=9$(分),方差是$\frac {1}{10}×[4×(10-9)^{2}+2×(8-9)^{2}+(7-9)^{2}+3×(9-9)^{2}]=1$(分²).
(3)
∵甲队成绩的方差是1.4分²,乙队成绩的方差是1分²,
∴成绩较为整齐的是乙队.
查看更多完整答案,请扫码查看


