《2025年同步练习册河北教育出版社九年级数学上册冀教版》

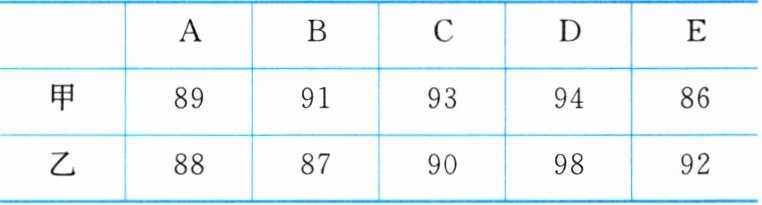
6. 九年级(一)班邀请 $A$,$B$,$C$,$D$,$E$ 五位评委对甲、乙两名同学的才艺表演打分,并组织全班 $50$ 名学生对两人进行民主测评投票,根据打分和投票情况绘制了如下的统计表和不完整的条形统计图：
五位评委的打分表

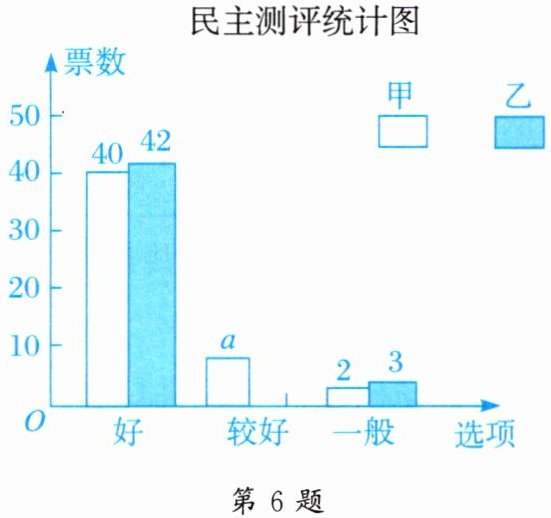
民主测评统计图

求得了五位评委对甲同学才艺表演所打分数的平均数和中位数分别为 $90.6$,$91$.
(1) 求五位评委对乙同学才艺表演所打分数的平均数和中位数.
(2) 求出 $a$ 的值,并补全条形统计图.
(3) 为了从甲、乙两人中选拔出一人去参加艺术节演出,班级制订了如下的选拔规则：
选拔综合分高的同学去参加艺术节演出. 其中,综合分 $=$ 才艺分 $× k+$ 测评分 $×(1 - k)$.($0.4 \lt k \lt 0.8$)
才艺分 $=$ 五位评委所打分数中去掉一个最高分和一个最低分,再算平均分.
测评分 $=$ “好”票数 $× 2+$ “较好”票数 $× 1+$ “一般”票数 $× 0$.
① 当 $k = 0.6$ 时,通过计算说明应选拔哪名同学去参加艺术节演出.
② 通过计算说明 $k$ 的值不能是多少.

答案：
解:
(1)$\overline{x}_{乙}=\frac{88+87+90+98+92}{5}=91$，中位数是90.
(2)$a=50 - 40 - 2=8$.
补全条形统计图如图:

(3)①甲的才艺分$=\frac{89+91+93}{3}=91$，甲的测评分$=40× 2+8× 1+2× 0=88$，甲的综合分$=91× 0.6+88× (1 - 0.6)=89.8$.
乙的才艺分$=\frac{88+90+92}{3}=90$，乙的测评分$=42× 2+5× 1+2× 0=89$，乙的综合分$=90× 0.6+89× (1 - 0.6)=89.6$.
∵甲的综合分＞乙的综合分，
∴应选拔甲同学去参加艺术节演出.
②甲的综合分$=91k+88(1 - k)=3k+88$，乙的综合分$=90k+89(1 - k)=k+89$，若从甲、乙两人中选拔出一人去参加演出，则$3k+88≠k+89$，
∴$k≠0.5$.

7. 某校 $260$ 名学生参加植树活动,要求每人植 $4\sim7$ 棵,活动结束后随机抽查了 $20$ 名学生每人的植树量,并分为四种类型,$A$($4$ 棵),$B$($5$ 棵),$C$($6$ 棵),$D$($7$ 棵). 将各类的人数绘制成扇形图(如图①)和条形图(如图②),经确认扇形图是正确的,而条形图尚有一处错误.

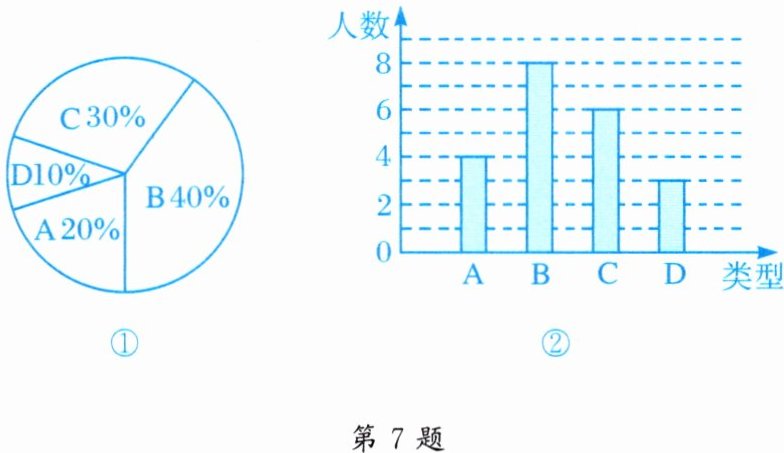
根据上述信息,回答下列问题：
(1) 写出条形图中存在的错误,并说明理由.
(2) 写出这 $20$ 名学生每人植树量的众数和中位数.
(3) 在求这 $20$ 名学生每人植树量的平均数时,小宇是这样分析的：
第一步：求平均数的公式是 $\overline{x}= \frac{x_{1}+x_{2}+… +x_{n}}{n}$；
第二步：在该问题中,$n = 4$,$x_{1} = 4$,$x_{2} = 5$,$x_{3} = 6$,$x_{4} = 7$；
第三步：$\overline{x}= \frac{4 + 5 + 6 + 7}{4}= 5.5$(棵).
① 小宇的分析是从哪一步开始出现错误的？
② 请你帮他计算出正确的平均数,并估计这 $260$ 名学生共植树多少棵.

答案： 解:
(1)类型D的人数应为2.
(2)众数为5棵，中位数为5棵.
(3)①第二步
②$n = 20$，$\overline{x}=\frac{4× 4+5× 8+6× 6+7× 2}{20}=5.3$(棵)，260名学生共植树$5.3× 260=1378$(棵).