《2025年亮点给力大试卷九年级数学上册苏科版》

1. 亮点原创 为了改善人口结构,落实积极应对人口老龄化国家战略,促进人口长期均衡发展,国家鼓励一对夫妻生育三个子女.现某对夫妻准备生育3个孩子(生男生女的概率相同,且与顺序无关),若该夫妻生育三胎,每胎都是1个小孩,则该夫妻生育的3个小孩是1男2女的概率是 (C)
A.$\frac{1}{8}$
B.$\frac{1}{4}$
C.$\frac{3}{8}$
D.$\frac{1}{2}$

答案： C

2. 亮点原创 为了宣传粮食安全,小明写了一份倡议书,通过社交平台传播.他设计了如下的传播规则:将倡议书发表在自己的社交平台上,再邀请n个好友转发,每个好友转发后,又邀请n个互不相同的好友转发,以此类推.若经过两轮转发后,共有91个人参与宣传,则n的值为 (A)
A.9
B.10
C.11
D.12

答案： A

3. 阅读下面的诗词然后解题:
大江东去浪淘尽,千古风流数人物.而立之年督东吴,早逝英年两位数.
十位恰小个位三,个位平方与寿符.哪位学子算得快,多少年华属周瑜?
请你通过列方程式,算出周瑜去世时的年龄是 (D)
A.25岁
B.30岁
C.35岁
D.36岁

答案： D

4. 阅读理解:如图①,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,则平面上任意一点M的位置可由∠MOx的度数θ与OM的长m确定,有序数对(θ,m)称为点M的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在如图②所示的极坐标系下,若正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为 (C)
A.(30°,2)
B.(45°,4)
C.(30°,2√{3})
D.(50°,2√{3})

答案： C

5. (2024·山东滨州)刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,在Rt△ABC中,∠C= 90°,AB,BC,CA的长分别为c,a,b,用含c,a,b的式子表示△ABC的内切圆直径d,则下列错误的是$ ( )A. d= a+b-cB. d= \frac{2ab}{a+b+c}C. d= \sqrt{2(c-a)(c-b)}D. d= $|(a-b)(c-b)|

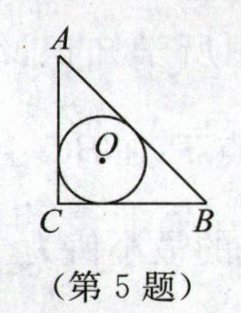
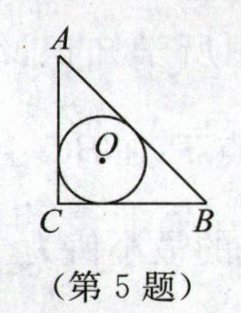
答案：
D 解析:如图,设$\odot O$与$\triangle ABC$三边的切点分别为D,E,F,连接OD,OE,OF,OA,OB,OC,易证四边形OECD是正方形.设$OE=OD=OF=r$,则$EC=CD=r$.又$AC=b$,$BC=a$,$AB=c$,所以$AF=AE=AC-CE=b-r$,$BF=BD=BC-CD=a-r$.因为$AF+BF=AB$,所以$b-r+a-r=c$,即$r=\frac{a+b-c}{2}$.所以$d=2r=a+b-c$.故A正确;因为$S_{\triangle ABC}=S_{\triangle AOC}+S_{\triangle BOC}+S_{\triangle AOB}$,且$\angle ACB=90^{\circ}$,所以$\frac{1}{2}ab=\frac{1}{2}br+\frac{1}{2}ar+\frac{1}{2}cr$.所以$ab=ar+br+cr$,即$r=\frac{ab}{a+b+c}$.所以$d=2r=\frac{2ab}{a+b+c}$.故B正确;因为$d=a+b-c$,所以$d^{2}=(a+b-c)^{2}=(a+b)^{2}-2c(a+b)+c^{2}=a^{2}+2ab+b^{2}-2ac-2bc+c^{2}$.在$\text{Rt}\triangle ABC$中,由勾股定理,得$a^{2}+b^{2}=c^{2}$,所以$d^{2}=2c^{2}+2ab-2ac-2bc=2(c^{2}+ab-ac-bc)=2[(c^{2}-ac)+b(a-c)]=2(c-a)(c-b)$.所以$d=\sqrt{2(c-a)(c-b)}$.故C正确;由已知条件无法证得$d=|(a-b)(c-b)|$.故D错误.