《2025年亮点给力大试卷九年级数学上册苏科版》

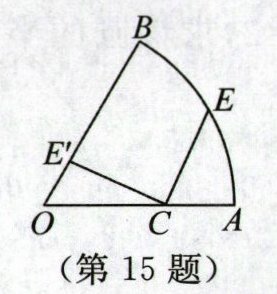
15. (2025·江苏苏州模拟)如图,在扇形 OAB 中,$∠AOB= 60^{\circ },OA= 4\sqrt {3}+8$,E 为$\widehat {AB}$的中点,C 为半径 OA 上一点,将线段 CE 绕点 C 逆时针旋转$90^{\circ }得到线段CE'$. 若点$E'$恰好落在半径 OB 上,则$OE'= $______.


4

答案： 解：设 $ OE' = x $，以 $ O $ 为原点，$ OA $ 为 $ x $ 轴建立坐标系。
∵ $ ∠AOB = 60^\circ $，$ E' $ 在 $ OB $ 上，
∴ $ E'\left( \frac{x}{2}, \frac{\sqrt{3}x}{2} \right) $。
∵ $ CE \perp CE' $ 且 $ CE = CE' $，设 $ C(a, 0) $，则 $ E\left( a + \frac{\sqrt{3}x}{2}, a - \frac{x}{2} \right) $。
∵ $ E $ 为 $ \widehat{AB} $ 中点，$ ∠AOE = 30^\circ $，$ OE = OA = 4\sqrt{3} + 8 $，
∴ $ E $ 坐标满足 $ x_E = OE \cos 30^\circ = 6 + 4\sqrt{3} $，$ y_E = OE \sin 30^\circ = 4 + 2\sqrt{3} $。
联立方程：
$ a + \frac{\sqrt{3}x}{2} = 6 + 4\sqrt{3} $
$ a - \frac{x}{2} = 4 + 2\sqrt{3} $
解得 $ x = 4 $。
答案：4

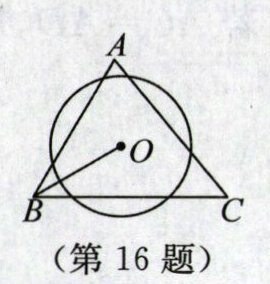
16. 亮点原创·如图,在$\triangle ABC$中,$∠ABC= 60^{\circ },\triangle ABC的三条边截\odot O$所得弦长相等,连接 OB. 若$\triangle ABC$的周长为 32,$OB= 6$,则$\triangle ABC$的面积为______48.

答案： 解：过点O作OD⊥BC于D，OE⊥AC于E，OF⊥AB于F，连接OA，OC。
∵△ABC的三条边截⊙O所得弦长相等，
∴OD=OE=OF=r（设为r），即O是△ABC的内心。
∵∠ABC=60°，
∴∠ABO=∠CBO=30°。
在Rt△OBD中，OB=6，∠OBD=30°，
∴OD=OB·sin30°=6×1/2=3，即r=3。
设△ABC的三边分别为a，b，c，周长a+b+c=32，
则半周长p=(a+b+c)/2=16。
∵S△ABC=pr=16×3=48。
答案：48

17. 如图,正方形纸片 ABCD 的边长为 8,$\odot O$的半径为 2,O 是该正方形的中心,将纸片按图示方式折叠,使$EA'恰好与\odot O$相切于点$A'(\triangle EFA'与\odot O$除切点外无重叠部分),延长$FA'交\odot O$于点 N,交边 CD 于点 G,则$A'G$的长是______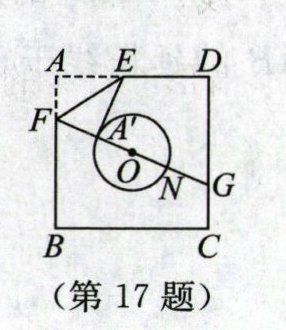4.

答案： 1. 首先，连接$OA'$：
因为$EA'$与$\odot O$相切于点$A'$，所以$OA'\perp EA'$。
设$OA'$的延长线交$BC$于点$M$，由于$O$是正方形$ABCD$的中心，正方形边长$a = 8$，$\odot O$半径$r=2$，则$OM = 4 - 2=2$，$MC = 4$。
由折叠可知$\angle EA'F=\angle A = 90^{\circ}$，又$OA'\perp EA'$，所以$OA'// EA'$，$\angle FA'O = 90^{\circ}$。
因为$ABCD$是正方形，所以$AD// BC$，$\angle D=\angle C = 90^{\circ}$，则$\angle FA'O=\angle C$。
又$\angle A'OG=\angle MOC$（对顶角相等）。
2. 然后，证明$\triangle A'OG\sim\triangle MOC$：
在$\triangle A'OG$和$\triangle MOC$中，$\left\{\begin{array}{l}\angle FA'O=\angle C\\\angle A'OG=\angle MOC\end{array}\right.$，所以$\triangle A'OG\sim\triangle MOC$（两角分别相等的两个三角形相似）。
根据相似三角形的性质$\frac{A'O}{MO}=\frac{A'G}{MC}$。
3. 最后，计算$A'G$的长度：
已知$A'O = 2$，$MO = 2$，$MC = 4$。
由$\frac{A'O}{MO}=\frac{A'G}{MC}$，即$\frac{2}{2}=\frac{A'G}{4}$。
所以$A'G = 4$。

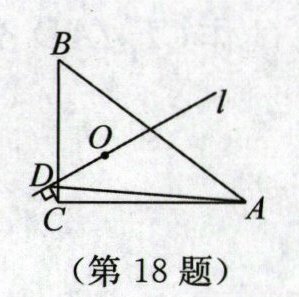
18. (2025·江苏扬州期末)如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ },BC= 3,AC= 4$,直线 l 经过$\triangle ABC$的内心 O,过点 C 作$CD⊥l$,垂足为 D,连接 AD,则 AD 的长的最小值是______.

$2\sqrt{2}$

答案： 解：在$Rt\triangle ABC$中，$∠ACB=90^{\circ}$，$BC=3$，$AC=4$，则$AB=\sqrt{AC^2 + BC^2}=\sqrt{4^2 + 3^2}=5$。
$\triangle ABC$的内切圆半径$r = \frac{AC + BC - AB}{2} = \frac{4 + 3 - 5}{2}=1$，内心$O$到$AC$、$BC$的距离均为$1$。
以$C$为原点，$CA$为$x$轴，$CB$为$y$轴建立坐标系，则$C(0,0)$，$A(4,0)$，$O(1,1)$。
因为$CD⊥l$，$O$在$l$上，所以点$D$的轨迹是以$OC$为直径的圆（$∠CDO=90^{\circ}$），圆心为$OC$中点$M\left(\frac{1}{2},\frac{1}{2}\right)$，半径$R = \frac{1}{2}OC = \frac{1}{2}\sqrt{1^2 + 1^2}=\frac{\sqrt{2}}{2}$。
$AD$的最小值为$AM - R$，其中$AM = \sqrt{\left(4 - \frac{1}{2}\right)^2 + \left(0 - \frac{1}{2}\right)^2}=\sqrt{\left(\frac{7}{2}\right)^2 + \left(-\frac{1}{2}\right)^2}=\frac{5\sqrt{2}}{2}$。
所以$AD_{\text{min}}=\frac{5\sqrt{2}}{2}-\frac{\sqrt{2}}{2}=2\sqrt{2}$。
$2\sqrt{2}$

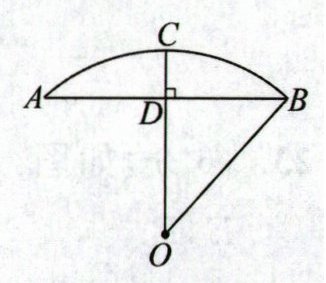
19. (6 分)如图是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为$\widehat {AB}$,桥的跨度(弧所对的弦长)$AB= 26m$,设$\widehat {AB}$所在圆的圆心为 O,半径$OC⊥AB$,垂足为 D,拱高(弧的中点到弦的距离)$CD= 5m$,连接 OB.
(1) 直接判断 AD 与 BD 之间的数量关系;
(2) 求这座石拱桥主桥拱的半径.

答案：
(1) AD = BD
(2) 解：设这座石拱桥主桥拱的半径为 $ r $ m。
因为 $ OC \perp AB $，$ AB = 26 $ m，所以 $ BD = \frac{1}{2}AB = 13 $ m。
因为 $ CD = 5 $ m，所以 $ OD = OC - CD = (r - 5) $ m。
在 $ \text{Rt}\triangle OBD $ 中，由勾股定理得 $ OB^2 = OD^2 + BD^2 $，
即 $ r^2 = (r - 5)^2 + 13^2 $，
解得 $ r = 19.4 $。
答：这座石拱桥主桥拱的半径为 $ 19.4 $ m。

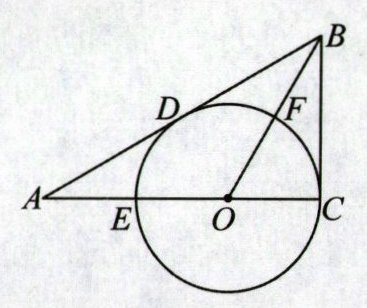
20. (6 分)(2024·湖北)如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ }$,点 E 在 AC 上,以 CE 的长为直径的$\odot O$交 AB 于点 D,交 OB 于点 F,且$BD= BC$.
(1) 求证:直线 AB 是$\odot O$的切线;
(2) 若$AD= \sqrt {3},AE= 1$,求$\widehat {CF}$的长.

答案： 1. （1）证明：
连接$OD$，$CD$。
因为$CE$是$\odot O$的直径，所以$\angle CDE = 90^{\circ}$，即$CD\perp AB$。
又因为$BD = BC$，根据等腰三角形三线合一的性质，$CD$是$\angle BCO$的平分线，所以$\angle BCD=\angle OCD$。
因为$OC = OD$，所以$\angle OCD=\angle ODC$，则$\angle BCD=\angle ODC$。
所以$OD// BC$。
因为$\angle ACB = 90^{\circ}$，即$BC\perp AC$，所以$OD\perp AB$。
又因为$OD$是$\odot O$的半径，所以直线$AB$是$\odot O$的切线。
2. （2）解：
设$\odot O$的半径为$r$，则$OC = OD=r$，$OA=r + 1$。
因为$OD\perp AD$，在$Rt\triangle ADO$中，根据勾股定理$OA^{2}=OD^{2}+AD^{2}$。
已知$AD = \sqrt{3}$，$AE = 1$，所以$(r + 1)^{2}=r^{2}+(\sqrt{3})^{2}$。
展开得$r^{2}+2r + 1=r^{2}+3$。
移项可得$2r=3 - 1$，解得$r = 1$。
因为$OD// BC$，所以$\triangle AOD\sim\triangle ACB$。
则$\frac{OD}{BC}=\frac{AO}{AC}$，$AC=AE + EC=1 + 2=3$，$AO=1 + 1=2$，$OD = 1$，所以$\frac{1}{BC}=\frac{2}{3}$，解得$BC=\frac{3}{2}$。
在$Rt\triangle BCD$中，$BD = BC=\frac{3}{2}$，$CD=\sqrt{BC^{2}-BD^{2}÷2}=\sqrt{(\frac{3}{2})^{2}-(\frac{3}{4})^{2}}=\frac{3\sqrt{3}}{4}$（利用等腰三角形三线合一，$CD\perp AB$，$AD=\sqrt{3}$，$AB=AD + BD=\sqrt{3}+\frac{3}{2}$，再由$\triangle AOD\sim\triangle ACB$也可求$\cos A=\frac{AD}{AO}=\frac{\sqrt{3}}{2}$，$\angle A = 30^{\circ}$，因为$OD// BC$，所以$\angle AOD=\angle ACB = 90^{\circ}$，$\angle A=\angle OBC = 30^{\circ}$，$\angle BOC = 60^{\circ}$。
根据弧长公式$l=\frac{n\pi R}{180}$（$n$是圆心角，$R$是半径），这里$n = 60^{\circ}$，$R = 1$。
所以$\widehat{CF}$的长$l=\frac{60\pi×1}{180}=\frac{\pi}{3}$。
综上，（1）得证；（2）$\widehat{CF}$的长为$\frac{\pi}{3}$。