《2025年亮点给力大试卷九年级数学上册苏科版》

6. 亮点原创·为弘扬和传承中华民族的传统文化,在春节即将到来之际,某书法协会开展“墨香氤氲,情系春节”活动,共有12位书法家到场写对联.最终经统计,有3位书法家各写了17副对联,5位书法家各写了13副对联,4位书法家各写了16副对联,则平均每位书法家写对联的副数为15.

答案： 15

7. (2024·内蒙古呼和浩特改编)我国南宋数学家杨辉在《田亩比类乘除捷法》中记录了这样一个问题:“直田积八百六十四步,只云阔与长共六十步,问阔及长各几步?”其大意如下:矩形的面积是864平方步,其中宽与长的和为60步,问宽和长各几步? 若设长为x步,则x的值为36.

答案： 36

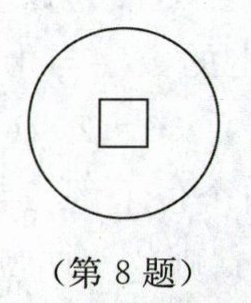
8. 张旭一家来到西安的碑林书画街欣赏字画,张旭在这里看到一幅《卖油翁》的画,画上有这样一段文字:“乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.”可见其卖油技艺之高.如图,若铜钱的半径为2cm,中间有边长为1cm的正方形小孔,任意向该铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是$\frac{1}{4\pi}$.

答案： $\frac{1}{4\pi}$

9. (2023·湖南常德)沈括的《梦溪笔谈》是我国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,$\widehat {AB}$是以点O为圆心,OA的长为半径的圆弧,C是弦AB的中点,点D在$\widehat {AB}$上,CD⊥AB.“会圆术”给出$\widehat {AB}$的长l的近似值s的计算公式:$s= AB+\frac {CD^{2}}{OA}$,当OA= 2,$∠AOB= 90^{\circ }$时,$|l-s|\approx$0.1.(结果保留一位小数)

答案： 0.1

10. 如图①,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,在此图形中连接四条线段得到如图②所示的图案,记阴影部分的面积为$S_{1}$,空白部分的面积为$S_{2}$,大正方形的边长为m,小正方形的边长为n.若$S_{1}= S_{2}$,则$\frac {n}{m}$的值为______.

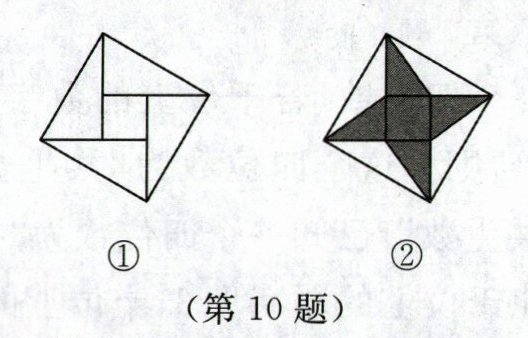
$\frac{\sqrt{3}-1}{2}$

答案： $\frac{\sqrt{3}-1}{2}$ 解析:设直角三角形的短直角边长为a.由题意,得$S_{2}=4×\frac{1}{2}a^{2}=2a^{2}$,$S_{1}=n^{2}+4×\frac{1}{2}an=n^{2}+2an$,大正方形的面积为$m^{2}=S_{1}+S_{2}$.又$S_{1}=S_{2}$,所以$m^{2}=2S_{2}=4a^{2}$,$n^{2}+2an=2a^{2}$,解得$m=2a$,$n=(\sqrt{3}-1)a$(负值已舍去).则$\frac{n}{m}=\frac{\sqrt{3}-1}{2}$.

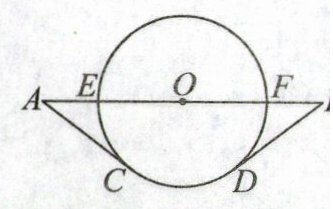
11. (16分)(2024·江苏宿迁期中)抖空竹是中国传统文化苑中一株灿烂的花朵,是国家级的非物质文化遗产之一,可见于全国各地,天津、北京、辽宁、吉林、黑龙江等地尤为盛行.在学习了圆之后,数学兴趣小组的同学对抖空竹进行了探究,其示意图如图所示.已知绳AC,BD分别与空竹截面图$\odot O$相切于C,D两点,连接左右两边绳上A,B两点,且AB经过圆心O,交$\odot O$于E,F两点,AE= BF.
(1) 求证:AC= BD;
(2) 若AE= 4,AC= 8,求A,B两点之间的距离.

答案： （1）连接OC,OD.因为AC,BD分别与$\odot O$相切于C,D两点,所以$OC\perp AC$,$OD\perp BD$,即$\angle ACO=\angle BDO=90^{\circ}$.又$OC=OD=OE=OF$,$AE=BF$,所以$AE+OE=BF+OF$,即$OA=OB$.所以$\text{Rt}\triangle AOC\cong\text{Rt}\triangle BOD$（HL）.所以$AC=BD$.
（2）设$\odot O$的半径为r,则$OC=OE=OF=r$.又$AE=4$,所以$OA=OE+AE=r+4$.由（1）,得$\angle ACO=90^{\circ}$,所以在$\text{Rt}\triangle AOC$中,$AC=8$,由勾股定理,得$AC^{2}+OC^{2}=OA^{2}$,即$8^{2}+r^{2}=(r+4)^{2}$,解得$r=6$.则$OE=OF=6$.又$BF=AE$,$AB=AE+OE+OF+BF$,所以$AB=20$.