《2025年亮点给力大试卷九年级数学上册苏科版》

24. (8分)
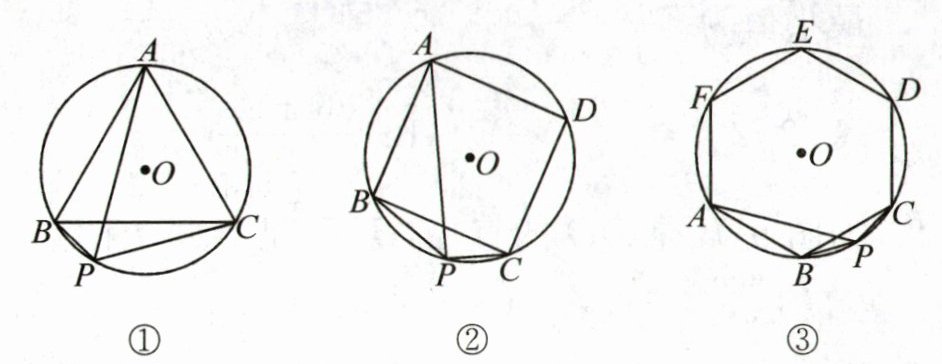
(1) 如图①,△ABC是⊙O的内接正三角形,P为$\overset{\frown}{BC}$上一动点,求证:PA= PB+PC;
(2) 如图②,四边形ABCD是⊙O的内接正方形,P为$\overset{\frown}{BC}$上一动点,求证:$PA= \sqrt{2}PB+PC$;
(3) 如图③,六边形ABCDEF是⊙O的内接正六边形,P为$\overset{\frown}{BC}$上一动点,请探究PA,PB,PC三者之间有何数量关系,并给予证明.

答案：
(1)因为△ABC是正三角形,所以BA = BC,∠ABC = ∠ACB = 60°.又∠APB = ∠ACB,所以∠APB = 60°.在PA上取一点Q,使PQ = PB,连接BQ,则△PBQ是正三角形.所以PB = QB,∠PBQ = 60°,即∠PBQ = ∠ABC,所以∠PBQ - ∠CBQ = ∠ABC - ∠CBQ,即∠PBC = ∠QBA.所以△CBP≌△ABQ (SAS).所以PC = QA.又PA = PQ + QA,所以PA = PB + PC.
(2)过点B作BM⊥BP,交PA于点M,连接AC,则∠PBM = 90°.因为四边形ABCD是正方形,所以AB = CB,∠ABC = 90°,∠ACB = 45°,即∠PBM = ∠ABC.所以∠PBM - ∠CBM = ∠ABC - ∠CBM,即∠PBC = ∠MBA.又∠APB = ∠ACB,所以∠APB = 45°.又∠PMB + ∠APB = 90°,所以∠PMB = 45°,即∠PMB = ∠APB.所以PB = MB.所以△ABM≌△CBP (SAS).所以MA = PC.在Rt△BPM中,由勾股定理,得PB² + MB² = PM²,所以$PM=\sqrt{2}PB$.又PA = PM + MA,所以$PA=\sqrt{2}PB + PC$.
(3)$PA=\sqrt{3}PB + PC$,证明如下:在PA上取一点N,使NA = PC,连接AC,BN.因为六边形ABCDEF是正六边形,所以∠ABC = 120°,AB = CB,即∠BAC = ∠BCA.又∠BAC + ∠BCA + ∠ABC = 180°,所以∠BCA = 30°,即∠BPA = 30°.又∠BAP = ∠BCP,所以△ABN≌△CBP (SAS).所以NB = PB.过点B作BH⊥PA于点H,则PN = 2PH,$BH=\frac{1}{2}PB$.在Rt△PBH中,由勾股定理,得$PH=\sqrt{PB^2 - BH^2}=\frac{\sqrt{3}}{2}PB$,所以PN = $\sqrt{3}PB$.又PA = PN + NA,所以$PA=\sqrt{3}PB + PC$.

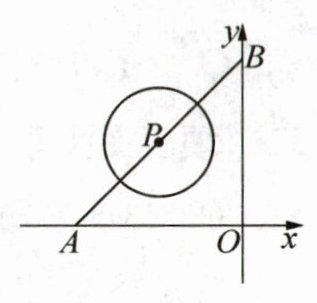
25. (8分)新趋势 推导探究 如图,一次函数y= x+4的图像分别交x轴、y轴于A,B两点,P为线段AB上的一动点,以点P为圆心,r为半径画圆.
(1) 若点P的横坐标为-3,当⊙P与x轴相切时,求半径r的值并判断此时⊙P与y轴的位置关系;
(2) 若$r= \frac{5}{2}$,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.

答案：
(1)由题意,把x = -3代入y = x + 4中,得y = 1.所以点P的坐标为(-3,1),即此时点P到x轴的距离为1,到y轴的距离为3.所以当⊙P与x轴相切时,r的值为1,即此时⊙P与y轴相离.
(2)因为⊙P与坐标轴有且只有3个公共点,所以有⊙P与x轴相切,与y轴相交、⊙P与y轴相切,与x轴相交和⊙P过原点，与x轴，y轴另各有一个交点这三种情况.若⊙P与x轴相切,与y轴相交,则点P的纵坐标是$\frac{5}{2}$.把$y=\frac{5}{2}$代入y = x + 4中,解得$x=-\frac{3}{2}$,$|-\frac{3}{2}|\lt\frac{5}{2}$,所以点P的坐标为$(-\frac{3}{2},\frac{5}{2})$;若⊙P与y轴相切,与x轴相交,则点P的横坐标是$-\frac{5}{2}$.把$x=-\frac{5}{2}$代入y = x + 4中,得$y=\frac{3}{2}$,$\frac{3}{2}\lt\frac{5}{2}$,所以点P的坐标为$(-\frac{5}{2},\frac{3}{2})$;若⊙P经过原点，因为∠AOB = 90°,所以∠AOB所对的弦必是⊙P的直径.则当AB为⊙P的直径时满足.此时P即为AB的中点.由题意，得点A的坐标为(-4,0),点B的坐标为(0,4).所以OA = OB = 4.由勾股定理，得$AB=\sqrt{OA^2 + OB^2}=4\sqrt{2}$,此时⊙P的半径为$2\sqrt{2}$.又⊙P的半径$r=\frac{5}{2}$,且$2\sqrt{2}\neq\frac{5}{2}$,所以此情况不存在.综上，点P的坐标为$(-\frac{3}{2},\frac{5}{2})$或$(-\frac{5}{2},\frac{3}{2})$.

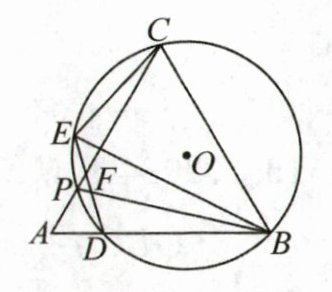
26. (8分)如图,P是等边三角形ABC的边AC上的动点(0°＜∠ABP＜30°),作△BCP的外接圆⊙O交AB于点D,E是⊙O上一点,且$\overset{\frown}{PD}= \overset{\frown}{PE}$,连接DE,BE,CE,且DE交BP于点F.
(1) 求证:∠ADE= ∠BEC;
(2) 当点P运动变化时,∠BFD的度数是否变化? 若变化,请说明理由;若不变,求∠BFD的度数;
(3) 探究线段BF,CE,EF之间的数量关系,并证明.

答案：
(1)连接PE.因为△ABC为等边三角形,所以∠A = ∠BCP = ∠DBC = 60°,BA = BC.因为$\overset{\frown}{PD}=\overset{\frown}{PE}$,所以∠ABP = ∠EBP.又∠BEP = ∠BCP = 60°,所以∠A = ∠BEP.又BP = BP,所以△ABP≌△EBP (AAS).所以BE = BA,即BE = BC.所以∠BEC = ∠BCE.因为四边形BCED是⊙O的内接四边形,所以∠BCE + ∠BDE = 180°.又∠ADE + ∠BDE = 180°,所以∠ADE = ∠BCE,即∠ADE = ∠BEC.
(2)∠BFD的度数不变.连接PE.因为$\overset{\frown}{PD}=\overset{\frown}{PE}$,所以∠DEP = ∠PBE.因为∠BFD = ∠BED + ∠PBE,∠BEP = ∠BED + ∠DEP,所以∠BFD = ∠BEP.由
(1),得∠BEP = 60°,所以∠BFD = 60°,即∠BFD的度数不变.
(3)BF = CE + EF.证明如下:如图,延长CE,BP相交于点G.由
(1)
(2),得∠DBC = ∠BCP = 60°,∠BFD = 60°,所以$\overset{\frown}{BP}=\overset{\frown}{CD}$.由$\overset{\frown}{PD}=\overset{\frown}{PE}$,所以∠PBD = ∠PCE,$\overset{\frown}{BD}=\overset{\frown}{CP}$,即∠FBD = ∠GCP,BD = CP.因为四边形BCED是⊙O的内接四边形,所以∠DEC + ∠DBC = 180°,即∠DEC = 180° - ∠DBC = 120°.又∠DEC + ∠DEG = 180°,所以∠DEG = 180° - ∠DEC = 60°.又∠EFG = ∠BFD,所以∠EFG = 60°.又∠G + ∠EFG + ∠DEG = 180°,所以∠G = 180° - ∠EFG - ∠DEG = 60°,即∠G = ∠BFD = ∠EFG = ∠DEG.所以△BDF≌△CPG (AAS),△EFG是等边三角形,即EG = EF,BF = CG.又CG = CE + EG,所以BF = CE + EF.