《2025年亮点给力大试卷九年级数学上册苏科版》

1. (2025·江苏宿迁期末)若$x_{1},x_{2}是方程x^{2}+3x+c= 0$(c 为常数)的两个不相等的实数根,且满足$x_{1}\lt x_{2}＜1$,则 c 的取值范围是 (C)
A.$c＜-4$
B.$c＞-4$
C.$-4\lt c＜\frac {9}{4}$
D.$c＞\frac {9}{4}$

答案： C

2. 如图,在平面直角坐标系中,点 A 在 x 轴上,点 B 的坐标为$(1,0)$,且 C,D 两点在函数$y= \left\{\begin{array}{l} x+1(x≥0),\\ -\frac {1}{2}x+1(x＜0)\end{array} \right. $的图像上.若在矩形 ABCD 内任意取一点,则此点取自阴影部分的概率是 (A)
A.$\frac {1}{4}$
B.$\frac {1}{3}$
C.$\frac {3}{8}$
D.$\frac {1}{2}$

答案： A

3. (2024·山东日照)如图,在菱形 ABCD 中,$AB= 2,∠B= 120^{\circ }$,点 O 是对角线 AC 的中点,以点 O 为圆心,OA 长为半径作圆心角为$60^{\circ }$的扇形 OEF,点 D 在扇形 OEF 内部,则图中阴影部分的面积为 ( )

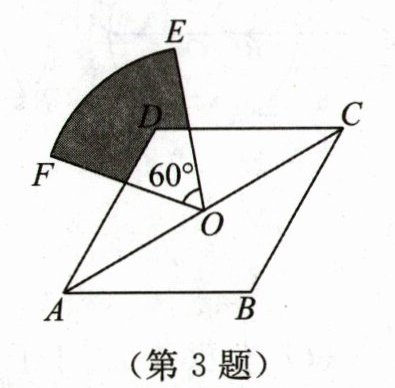
A.$\frac {π}{2}-\frac {\sqrt {3}}{4}$
B.$π-\frac {\sqrt {3}}{4}$
C.$\frac {π}{2}-\frac {1}{4}$
D.无法确定

答案：
A 解析:如图,过点 O 分别作 ON⊥AD 于点 N,OM⊥CD 于点 M,连接 OD,令 OE 交 CD 于点 G,OF 交 AD 于点 H,则∠ONH = ∠OMG = 90°.因为四边形 ABCD 是菱形,AB = 2,∠B = 120°,O 是 AC 的中点,所以 DO⊥AC,∠ADC = ∠B = 120°,CD = AB = 2,DO 平分∠ADC,OA = OC,即 OM = ON.又∠FOE = 60°,所以∠ADC + ∠FOE = 180°.又∠ADC + ∠FOE + ∠NHO + ∠DGO = 360°,所以∠NHO + ∠DGO = 360° - (∠ADC + ∠FOE) = 180°.因为∠DGO + ∠MGO = 180°,所以∠NHO = ∠MGO.所以△ONH≌△OMG(AAS).所以 S△ONH = S△OMG.所以 S△ONH + S四边形ONDG = S△OMG + S四边形ONDG,即 S四边形HOGD = S四边形NOMD.易得△ODN≌△ODM.所以 S四边形HOGD = S四边形NOMD = 2S△OMD.又∠ODC = $\frac{1}{2}$∠ADC = 60°,所以∠DCO = 90° - ∠ODC = 30°,即 OD = $\frac{1}{2}$CD = 1.所以 OA = OC = $\sqrt{CD^{2} - OD^{2}}$ = $\sqrt{3}$.同理,得∠DOM = 90° - ∠ODC = 30°,即 DM = $\frac{1}{2}$OD = $\frac{1}{2}$.所以 OM = $\sqrt{OD^{2} - DM^{2}}$ = $\frac{\sqrt{3}}{2}$.所以 S四边形HOGD = 2S△OMD = 2×$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$ = $\frac{\sqrt{3}}{4}$.所以 S影 = S扇形OFE - S四边形HOGD = $\frac{60π×(\sqrt{3})^{2}}{360}$ - $\frac{\sqrt{3}}{4}$ = $\frac{π}{2}$ - $\frac{\sqrt{3}}{4}$.

4. 亮点原创·如图,在平面直角坐标系中,O 为坐标原点,点 C 的坐标为$(0,8)$,点 A 的坐标为$(6,0),\odot A$的半径为 4,P 为$\odot A$上任意一点,E 是 PC 的中点,则 OE 的长的最大值为 ( )

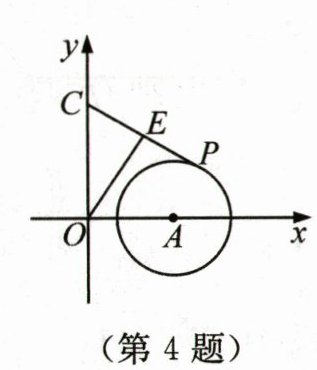
A.10
B.5
C.14
D.7

答案：
D 解析:如图,连接 AC,AP,取 AC 的中点 H,连接 EH,OH.因为 E 是 PC 的中点,所以 EH 是△ACP 的中位线.所以 EH = $\frac{1}{2}$AP.又⊙A 的半径为 4,所以 AP = 4,即 EH = 2.所以点 E 的运动轨迹是以点 H 为圆心,2 为半径的圆.因为点 C 的坐标为(0,8),点 A 的坐标为(6,0),所以 OC = 8,OA = 6.在 Rt△AOC 中,由勾股定理,得 AC = $\sqrt{OC^{2} + OA^{2}}$ = 10.所以 OH = $\frac{1}{2}$AC = 5.当点 E 在线段 OH 的延长线上时,OE 的长取最大值,且最大值为 OH + EH = 7.

5. 如图,在$Rt△ABC$中,$∠C= 90^{\circ },AC= 4π,BC= 3π$,半径是 2 的$\odot O$从与 AC 相切于点 D 的位置出发,在$△ABC$外部按顺时针方向沿三角形滚动.若第一次回到与 AC 相切于点 D 的位置,则$\odot O$共自转了 (C)
A.2 周
B.3 周
C.4 周
D.5 周

答案： C 解析:在 Rt△ABC 中,∠C = 90°,AC = 4π,BC = 3π,由勾股定理,得 AB = $\sqrt{AC^{2} + BC^{2}}$ = 5π.所以⊙O 在△ABC 的三边上共自转了 $\frac{3π + 4π + 5π}{2×π}$ = 3(周).又⊙O 绕过了△ABC 的三个外角,所以⊙O 自转了 360°,即 1 周.所以⊙O 共自转了 3 + 1 = 4(周).

6. 亮点原创·设方程$(y+2)(y+12)+(y+12)(y+22)+(y+2)(y+22)= 0的两根分别为y_{1},y_{2}$,则$(y_{1}+2)\cdot (y_{2}+2)= $$\frac{200}{3}$.

答案： $\frac{200}{3}$