《2025年亮点给力大试卷九年级数学上册苏科版》

25. (10分)节日期间,某商场为吸引顾客,开展购物抽奖活动.如图,一可自由转动的圆盘被平均分成16个扇形,每个扇形都标有数,顾客在该商场一次性购物每满500元可免费转动圆盘一次,当圆盘自动停止时,指针所指的数,即为商场奖励给顾客的金额数.某顾客在该商场一次性购物900元.
(1) 该顾客转动一次转盘获得100元奖励的概率是______$\frac{1}{8}$;
(2) 如果你是该顾客,那么你会选择参加一次抽奖还是再购买100元的商品参加两次抽奖?做出你的选择并简单说明理由.
再购买100元的商品参加两次抽奖.理由如下:由题图，得$P$(获得200元)$=\frac{1}{16}$，$P$(获得100元)$=\frac{2}{16}=\frac{1}{8}$，$P$(获得50元)$=\frac{3}{16}$，$P$(获得10元)$=\frac{4}{16}=\frac{1}{4}$，$P$(获得5元)$=\frac{6}{16}=\frac{3}{8}$，所以抽奖一次平均获得$\frac{1}{16}×200+\frac{1}{8}×100+\frac{3}{16}×50+\frac{1}{4}×10+\frac{3}{8}×5 = 38.75$(元).若抽奖一次，则获奖金额与购物金额的比为$\frac{38.75}{900}=\frac{155}{3600}$；若抽奖两次，则获奖金额与购物金额的比为$\frac{38.75×2}{1000}=\frac{77.5}{1000}=\frac{31}{400}=\frac{279}{3600}$.因为$\frac{279}{3600}＞\frac{155}{3600}$，所以再购买100元的商品参加两次抽奖更合算.

答案：
(1)$\frac{1}{8}$
(2)再购买100元的商品参加两次抽奖.理由如下:由题图，得$P$(获得200元)$=\frac{1}{16}$，$P$(获得100元)$=\frac{2}{16}=\frac{1}{8}$，$P$(获得50元)$=\frac{3}{16}$，$P$(获得10元)$=\frac{4}{16}=\frac{1}{4}$，$P$(获得5元)$=\frac{6}{16}=\frac{3}{8}$，所以抽奖一次平均获得$\frac{1}{16}×200+\frac{1}{8}×100+\frac{3}{16}×50+\frac{1}{4}×10+\frac{3}{8}×5 = 38.75$(元).若抽奖一次，则获奖金额与购物金额的比为$\frac{38.75}{900}=\frac{155}{3600}$；若抽奖两次，则获奖金额与购物金额的比为$\frac{38.75×2}{1000}=\frac{77.5}{1000}=\frac{31}{400}=\frac{279}{3600}$.因为$\frac{279}{3600}＞\frac{155}{3600}$，所以再购买100元的商品参加两次抽奖更合算.

26. (10分)新素养 运算能力 (2025·江苏无锡期末)三个小球上分别标有-2,0,1三个数,这三个小球除所标的数不同外,其余均相同,将小球放入一个不透明的布袋中搅匀.
(1) 从布袋中任意摸出一个小球,将小球上所标的数记下,然后将小球放回布袋中,搅匀后从中再任意摸出一个小球,再记下小球上所标的数,求两次记下的数之和大于0的概率(请用画树状图法给出分析过程,并求出结果);
(2) 从

布

袋中任意摸出一个小球,将小球上所标的数记下,然后将小球放回布袋中,搅匀后从中再任意摸出一个小球,将小球上所标的数再记下……这样一共摸了13次.若记下的13个数之和等于-4,平方和等于14,求这13次摸球中,摸到球上所标的数是0的次数.

答案：

(1) 解：画树状图如下：

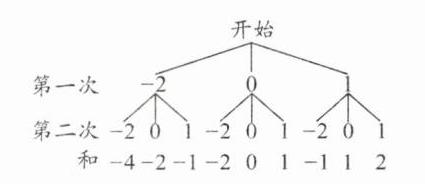
共有9种等可能的结果，其中两次记下的数之和大于0的结果有：(0,1)，(1,0)，(1,1)，共3种。
所以两次记下的数之和大于0的概率为：$ \frac{3}{9} = \frac{1}{3} $。
(2) 解：设摸到-2的次数为$ x $，摸到0的次数为$ y $，摸到1的次数为$ z $。
根据题意得：
$ \begin{cases} x + y + z = 13 \\-2x + 0 \cdot y + 1 \cdot z = -4 \\(-2)^2x + 0^2y + 1^2z = 14 \end{cases} $
化简得：
$ \begin{cases} x + y + z = 13 ① \\-2x + z = -4 ② \\4x + z = 14 ③ \end{cases} $
由②得：$ z = 2x - 4 ④ $
把④代入③得：$ 4x + 2x - 4 = 14 $，解得$ x = 3 $
把$ x = 3 $代入④得：$ z = 2×3 - 4 = 2 $
把$ x = 3 $，$ z = 2 $代入①得：$ 3 + y + 2 = 13 $，解得$ y = 8 $
所以摸到球上所标的数是0的次数为8。
答案：
(1) $ \frac{1}{3} $；
(2) 8。