《2025年亮点给力大试卷九年级数学上册苏科版》

14. (2024·浙江)有8张质地、大小完全相同的卡片,正面分别写着数1,2,3,4,5,6,7,8,将其洗匀后背面朝上放于桌面.若从中任意抽取1张,则该卡片上的数是4的整数倍的概率是$\frac{1}{4}$.

答案： $\frac{1}{4}$

15. (2025·江苏南京模拟)若关于x的方程$x^{2}-3x+m= 0$有两个不相等的实数根,且$m≥-3$,则从满足条件的所有整数m中任意选取一个,恰好是负数的概率是______$\frac{1}{2}$.

答案： $\frac{1}{2}$

16. (2025·江苏淮安期末)动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,据此若设刚出生的这种动物共有a只,则20年后存活的有0.8a只,现年20岁的这种动物活到25岁的概率是0.625.

答案： 0.8a　$0.625$

17. 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,正方形边上的整点称为边整点.如图,第一个正方形有4个边整点,第二个正方形有8个边整点,第三个正方形有12个边整点……按此规律继续作下去.若从内向外共作了5个这样的正方形,则其边整点的个数共有60个,这些边整点落在函数$y= \frac{4}{x}$的图像上的概率是$\frac{1}{10}$.

答案： 60　$\frac{1}{10}$

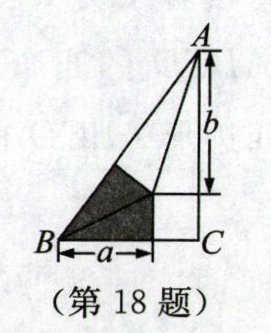
18. (2025·江苏徐州期末)我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理.如图,在$Rt△ABC$中,$∠C= 90^{\circ}$,若$a= 2,b= 3$,现任意向该图形内掷一枚小针(若掷到边界上,则重掷),则针尖落在阴影区域内的概率为______.

$\frac{1}{3}$

答案： $\frac{1}{3}$　解析:设正方形的边长为$x$.因为$a = 2$，$b = 3$，所以$AB = 2 + 3 = 5$，$BC = 2 + x$，$AC = 3 + x$.在$\text{Rt}\triangle ABC$中，由勾股定理，得$AC^{2}+BC^{2}=AB^{2}$，所以$(x + 3)^{2}+(2 + x)^{2}=5^{2}$，解得$x_{1}=1$，$x_{2}=-6$(不符合题意，舍去).所以$BC = 3$，$AC = 4$.所以$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC = 6$，$S_{\text{阴影}}=2×\frac{1}{2}ax = 2$.所以针尖落在阴影区域内的概率为$\frac{2}{6}=\frac{1}{3}$.

19. (6分)(2025·江苏无锡模拟)在一个不透明的布袋中装有三个小球,小球上分别标有数字0,1,2,它们除所标数字外其他都相同.搅匀后小明先从布袋中任意摸出一个小球,记下数字作为平面直角坐标系内点A的横坐标,将此球放回、搅匀,再从布袋中任意摸出一个小球,记下数字作为平面直角坐标系内点A的纵坐标.请用画树状图或列表的方法列举出点A所有可能的坐标,并求出点A在坐标轴上的概率.

答案： 列表如下:
点$A$的坐标
横坐标 纵坐标
0 1 2
0 $(0,0)$ $(0,1)$ $(0,2)$
1 $(1,0)$ $(1,1)$ $(1,2)$
2 $(2,0)$ $(2,1)$ $(2,2)$
由表格，得点$A$的所有可能的坐标为$(0,0)$，$(1,0)$，$(2,0)$，$(0,1)$，$(1,1)$，$(2,1)$，$(0,2)$，$(1,2)$，$(2,2)$，共9种，且每种结果的可能性相等，其中点$A$在坐标轴上的结果有5种，则点$A$在坐标轴上的概率为$\frac{5}{9}$.