《2025年亮点给力大试卷九年级数学上册苏科版》

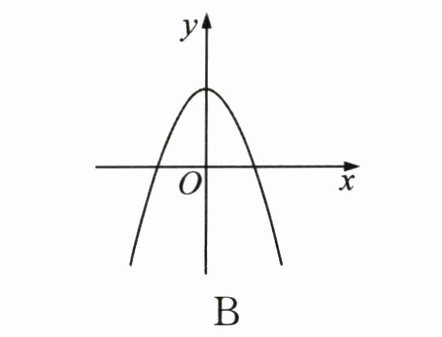
9. 若 $ A(-4, m - 2) $, $ B(-2, m) $, $ C(2, m) $三点在同一函数图像上,则该函数图像可能是 (B)

答案： B

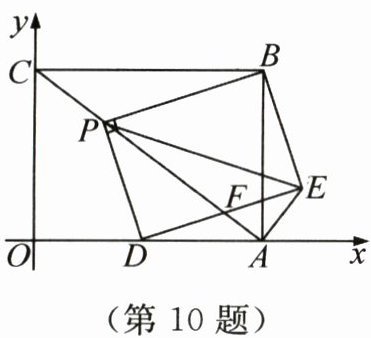
10. 新素养 推理能力 如图,直线 $ y = -\frac{3}{4}x + 6 $与 $ x $轴、 $ y $轴分别交于 $ A $, $ C $两点,点 $ B $的坐标为 $ (8, 6) $,连接 $ AB $, $ BC $, $ P $是线段 $ AC $(不含端点)上一动点,连接 $ BP $,过点 $ P $作 $ BP $的垂线交线段 $ OA $于点 $ D $,以 $ PB $, $ PD $为边作矩形 $ BPDE $, $ DE $与 $ AC $交于点 $ F $,连接 $ AE $。有下列结论：
① $ \tan \angle BAE = \frac{3}{4} $；② 连接 $ PE $,点 $ P $在移动过程中, $ 6 \leq PE \leq 10 $；③ 当 $ CP = 5 $时, $ FP = FE $；
④ 当线段 $ CF $的长取最小值时,点 $ P $的坐标为 $ (\frac{9}{5}, \frac{93}{20}) $。其中正确的有 ( )B

A.1个
B.2个
C.3个
D.4个

答案： B 解析:对于$y=-\frac{3}{4}x+6$，令$x=0$，得$y=6$；令$y=0$，得$-\frac{3}{4}x+6=0$，解得$x=8$。因为直线$y=-\frac{3}{4}x+6$与$x$轴、$y$轴分别交于$A$，$C$两点，所以点$A$的坐标为$(8,0)$，点$C$的坐标为$(0,6)$，即$OC = 6$，$OA = 8$。又点$B$的坐标为$(8,6)$，所以易得四边形$OABC$是矩形。所以$\angle OCB = \angle ABC = \angle OAB = 90^{\circ}$，$AB = OC = 6$，$BC = OA = 8$，$BC// OA$。连接$BD$。又四边形$BPDE$是矩形，所以$PD = BE$，$\angle BPD = \angle PDE = \angle BED = \angle PBE = 90^{\circ}$，即$B$，$P$，$D$，$A$，$E$五点共圆，$BD$为直径。所以$\angle PAE = \angle PDE = 90^{\circ}$，即$\angle PAB + \angle BAE = 90^{\circ}$。又$\angle PAB + \angle ACB = 90^{\circ}$，所以$\angle ACB = \angle BAE$。所以$\tan\angle BAE = \tan\angle ACB = \frac{AB}{BC} = \frac{3}{4}$。故①正确；连接$OB$。因为四边形$BPDE$是矩形，所以$PE = BD$。又$P$是线段$AC$（不含端点）上一动点，且点$D$在线段$OA$上，所以当$D$，$O$两点重合时，$BD$的长最大，最大值为$OB$的长。在$Rt\triangle OBC$中，由勾股定理，得$OB = \sqrt{OC^{2} + BC^{2}} = 10$，所以$BD$的长最大为$10$，即$PE$的长最大为$10$。此时$P$，$C$两点重合，不符合题意。当$BD\perp OA$，即$D$，$A$两点重合时，$BD$的长最小，最小值为$6$。所以点$P$在移动过程中，$6\leq PE\lt10$。故②错误；因为四边形$OABC$是矩形，所以$AC = OB = 10$。因为$CP = 5$，所以$P$为$AC$的中点。因为$\angle ABC = 90^{\circ}$，所以$AP = BP$。所以$\angle PAB = \angle PBA$。又$\angle PAB + \angle BAE = 90^{\circ}$，$\angle PBA + \angle ABE = 90^{\circ}$，所以$\angle BAE = \angle ABE$，即$AE = BE$。所以$PD = AE$。因为$B$，$P$，$D$，$A$，$E$五点共圆，所以$\angle DPA = \angle AED$。又$\angle PFD = \angle EFA$，所以$\triangle PFD\cong\triangle EFA$（AAS）。所以$FP = FE$。故③正确；过点$P$作$MN\perp OA$于点$N$，交$BC$于点$M$，过点$F$作$FH\perp OA$于点$H$。因为$OA// BC$，所以$MN\perp BC$。又$\angle CON = 90^{\circ}$，所以四边形$OCMN$是矩形。所以$MN = OC = 6$，$CM = ON$。又$\angle PCM = \angle ACB$，所以$\triangle CPM\backsim\triangle CAB$。所以$\frac{CM}{CB} = \frac{PM}{AB}$，即$\frac{CM}{PM} = \frac{CB}{AB} = \frac{4}{3}$。设$CM = 4m$，所以$PM = 3m$，$ON = 4m$，$BM = 8 - 4m$，即$PN = 6 - 3m$。同理，得$\frac{FH}{CO} = \frac{AH}{AO}$，即$\frac{FH}{AH} = \frac{CO}{AO} = \frac{3}{4}$。设$FH = 3a$，则$AH = 4a$。在$Rt\triangle AFH$中，由勾股定理，得$AF = \sqrt{FH^{2} + AH^{2}} = 5a$。因为$\angle BPM + \angle DPN = 180^{\circ} - \angle BPD = 90^{\circ}$，$\angle BPM + \angle PBM = 90^{\circ}$，所以$\angle PBM = \angle DPN$。又$\angle BMP = \angle PND = 90^{\circ}$，所以$\triangle BMP\backsim\triangle PND$。所以$\frac{BM}{PN} = \frac{PM}{DN}$，即$\frac{8 - 4m}{6 - 3m} = \frac{3m}{DN}$，解得$DN = \frac{9m}{4}$。经检验，$DN = \frac{9m}{4}$是原方程的解，且符合题意。所以$DH = OA - ON - DN - AH = 8 - \frac{25}{4}m - 4a$。同理，得$\triangle DHF\backsim\triangle PND$，所以$\frac{HF}{ND} = \frac{DH}{PN}$，即$\frac{3a}{\frac{9}{4}m} = \frac{8 - \frac{25}{4}m - 4a}{6 - 3m}$。整理，得$a = -\frac{25}{32}m^{2} + m$。又$-\frac{25}{32} \lt 0$，所以当$m = -\frac{1}{2×(-\frac{25}{32})} = \frac{16}{25}$时，$a$有最大值，即此时$CF = 10 - 5a$有最小值。此时点$P$的坐标为$(4m,6 - 3m)$，即$(\frac{64}{25},\frac{102}{25})$。故④错误。综上，正确的有$2$个。

11. 若关于 $ x $的一元二次方程 $ x^{2} - ax + 5 = 0 $有一个根是1,则 $ a = $6。

答案： 6

12. 抛物线 $ y = -3(x - 1)^{2} + 5 $的顶点坐标为(1,5)。

答案： (1,5)

13. 新素养 运算能力 小红沿坡比为 $ 1 : \sqrt{3} $的斜坡向上走了100 m,则她实际升高了50m。

答案： 50

14. 已知圆锥的底面圆半径为2 cm,母线长为5 cm,则它的侧面展开图的面积为10π $ cm^{2} $。

答案： 10π

15. 如图,四边形 $ ACBD $是 $ \odot O $的内接四边形,对角线 $ AB $, $ CD $相交于点 $ P $。若 $ PA = 2 $, $ PB = 6 $, $ PC = 3 $,则 $ PD = $4。

答案： 4

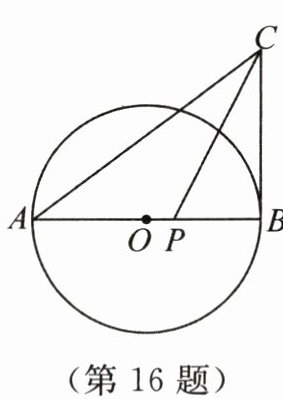
16. 如图, $ AB $是 $ \odot O $的直径, $ BC $切 $ \odot O $于点 $ B $, $ \angle ACB $的平分线交 $ AB $于点 $ P $。若 $ AC = 5 $, $ BC = 3 $,则 $ OP $的长为______1/2。

答案： 1/2

17. 如图,函数 $ G $的图像是由 $ y = x^{2} + 2x + 2(x \leq 0) $的图像 $ C_{1} $和它关于点 $ (0, 2) $成中心对称的图像 $ C_{2} $组成。若在函数 $ G $的图像上存在不重合的两点 $ A(a, y_{1}) $, $ B(b, y_{2}) $,且 $ a \lt 0 \lt b $, $ a + b = 0 $,使当 $ a \leq x \leq b $时,函数 $ G $的最大值和最小值均为定值,则 $ a $的取值范围为$-1 - \sqrt{2} \leq a \leq -1$。

答案： -1 - √2 ≤ a ≤ -1 解析:因为$y = x^{2} + 2x + 2 = (x + 1)^{2} + 1(x \leq 0)$，所以图像$C_1$的顶点坐标为$(-1,1)$。由题意，得图像$C_2$的开口向下，与图像$C_1$的形状完全相同，其顶点坐标为$(1,3)$，所以图像$C_2$的函数表达式为$y = -(x - 1)^{2} + 3 = -x^{2} + 2x + 2(x \gt 0)$。因为$a \lt 0 \lt b$，$a + b = 0$，所以$b = -a$，点$A(a,y_1)$和点$B(b,y_2)$关于点$(0,2)$对称。令$(x + 1)^{2} + 1 = 3$，解得$x = -\sqrt{2} - 1$（正值已舍去）；令$-(x - 1)^{2} + 3 = 1$，解得$x = \sqrt{2} + 1$（负值已舍去）。当$a \lt -\sqrt{2} - 1$时，$b \gt \sqrt{2} + 1$。结合题图可知当$x = a$时，函数$G$取最大值，且最大值为$a^{2} + 2a + 2$；当$x = b$时，函数$G$取最小值，且最小值为$-b^{2} + 2b + 2$。当$-\sqrt{2} - 1 \leq a \leq -1$时，$1 \leq b \leq \sqrt{2} + 1$，结合题图可知当$x = 1$时，函数$G$取最大值，且最大值为$3$；当$x = -1$时，函数$G$取最小值，且最小值为$1$，均为定值。当$-1 \lt a \lt 0$时，$0 \lt b \lt 1$，结合题图可知当$x = b$时，函数$G$取最大值，且最大值为$-b^{2} + 2b + 2$；当$x = a$时，函数$G$取最小值，且最小值为$a^{2} + 2a + 2$。又当$a \leq x \leq b$时，函数$G$的最大值和最小值均为定值，所以$a$的取值范围为$-\sqrt{2} - 1 \leq a \leq -1$。

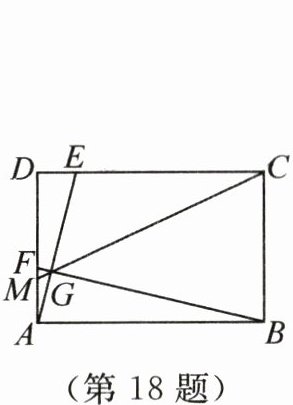
18. 如图,四边形 $ ABCD $为矩形, $ AB = 12 $, $ BC = 8 $,点 $ E $在边 $ DC $上从点 $ D $运动到点 $ C $,速度为每秒2个单位长度,点 $ F $同时从点 $ A $开始沿射线 $ AD $运动,速度为每秒3个单位长度,当点 $ E $停止时,点 $ F $也随之停止。连接 $ AE $, $ BF $交于点 $ G $,连接 $ CG $并延长,交直线 $ AD $于点 $ M $,则 $ AM $的长的最大值为______。

答案：
$\frac{9}{2}$ 解析:因为四边形$ABCD$是矩形，$AB = 12$，$BC = 8$，所以$\angle DAB = \angle ADC = 90^{\circ}$，$AD = BC = 8$，$CD = AB = 12$。由题意，设运动时间为$t$秒，则$DE = \frac{2t}{3t} = \frac{2}{3}$，$\frac{AD}{AB} = \frac{8}{12} = \frac{2}{3}$，所以$\frac{DE}{AF} = \frac{AD}{BA}$。所以$\triangle ADE\backsim\triangle BAF$。所以$\angle DAE = \angle ABF$。又$\angle DAE + \angle BAG = 90^{\circ}$，所以$\angle ABF + \angle BAG = 90^{\circ}$，即$\angle AGB = 180^{\circ} - (\angle ABF + \angle BAG) = 90^{\circ}$。所以点$G$在以$AB$为直径的圆上运动。如图，取$AB$的中点$O$，以点$O$为圆心，$AB$的长为直径画圆，作$\odot O$的切线$CH$，交$AD$于点$M'$，切点为$H$。又$CG$与$AD$相交于点$M$，所以$DM \geq DM'$，即$DM$的长的最小值为$DM'$的长。又$AM = AD - DM$，所以$AM = 8 - DM$，即此时$AM$的长最大，且最大值为$8 - DM'$。所以$CH = BC = 8$，$M'H = M'A$。设$DM' = x$，则$M'H = M'A = AD - DM' = 8 - x$。所以$CM' = CH + M'H = 16 - x$。在$Rt\triangle CDM'$中，由勾股定理，得$CM'^{2} = DM'^{2} + CD^{2}$，所以$(16 - x)^{2} = x^{2} + 12^{2}$，解得$x = \frac{7}{2}$。则$DM' = \frac{7}{2}$。所以$AM$的长的最大值为$8 - DM' = \frac{9}{2}$。