第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
1. (2023·山东东营)若圆锥侧面展开图的面积是15π,母线长是5,则这个圆锥的底面圆半径是 (
A.3
B.4
C.5
D.6
A
)A.3
B.4
C.5
D.6
答案:
A
2. 亮点原创已知5角硬币的直径约为20mm,则用一枚5角硬币能完全覆盖住的正方形的边长最大不能超过 (
A.5mm
B.5$\sqrt {2}$mm
C.10mm
D.10$\sqrt {2}$mm
D
)A.5mm
B.5$\sqrt {2}$mm
C.10mm
D.10$\sqrt {2}$mm
答案:
1. 首先明确:
当正方形的对角线长等于圆的直径时,这个正方形的边长最大(此时圆能完全覆盖正方形)。
设正方形的边长为$a$,根据正方形的性质,正方形的对角线$l$与边长$a$的关系为$l = \sqrt{a^{2}+a^{2}}$(由勾股定理$l^{2}=a^{2}+a^{2}$,$l\gt0$,$a\gt0$),即$l=\sqrt{2}a$。
2. 然后已知圆的直径$l = 20mm$:
因为$l=\sqrt{2}a$,且$l = 20mm$,所以$a=\frac{l}{\sqrt{2}}$。
将$l = 20mm$代入$a=\frac{l}{\sqrt{2}}$,根据分母有理化$a=\frac{20}{\sqrt{2}}=\frac{20\sqrt{2}}{\sqrt{2}×\sqrt{2}}$。
计算可得$a = 10\sqrt{2}mm$。
所以用一枚$5$角硬币能完全覆盖住的正方形的边长最大不能超过$10\sqrt{2}mm$,答案是D。
当正方形的对角线长等于圆的直径时,这个正方形的边长最大(此时圆能完全覆盖正方形)。
设正方形的边长为$a$,根据正方形的性质,正方形的对角线$l$与边长$a$的关系为$l = \sqrt{a^{2}+a^{2}}$(由勾股定理$l^{2}=a^{2}+a^{2}$,$l\gt0$,$a\gt0$),即$l=\sqrt{2}a$。
2. 然后已知圆的直径$l = 20mm$:
因为$l=\sqrt{2}a$,且$l = 20mm$,所以$a=\frac{l}{\sqrt{2}}$。
将$l = 20mm$代入$a=\frac{l}{\sqrt{2}}$,根据分母有理化$a=\frac{20}{\sqrt{2}}=\frac{20\sqrt{2}}{\sqrt{2}×\sqrt{2}}$。
计算可得$a = 10\sqrt{2}mm$。
所以用一枚$5$角硬币能完全覆盖住的正方形的边长最大不能超过$10\sqrt{2}mm$,答案是D。
3. 新趋势情境素材(2023·山西)如图为高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过A,B两点的两条切线相交于点C,列车在从点A到点B行驶的过程中转角α为60°.若半径OA= 1.5km,则⌢AB的长为 (

A.π/4km
B.π/2km
C.3π/4km
D.3π/8km
B
)
A.π/4km
B.π/2km
C.3π/4km
D.3π/8km
答案:
B
4. (2024·内蒙古呼和浩特)如图,正四边形ABCD和正五边形CEFGH都内接于⊙O,AD和EF相交于点M,则∠AMF的度数为 (
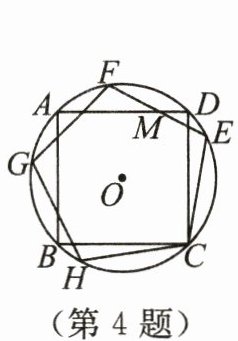
A.26°
B.27°
C.28°
D.30°
B
)
A.26°
B.27°
C.28°
D.30°
答案:
B
5. 如图,在菱形ABCD中,∠D= 60°,AB= 2,以点B为圆心,BC的长为半径画⌢AC,P为菱形内部一点,连接PA,PB,PC.当△BPC为等腰直角三角形时,图中阴影部分的面积为 (
$A.\frac {2}{3}π-\frac {\sqrt {3}+1}{2}$
$B.\frac {2π}{3}-\frac {\sqrt {3}*1}{2}$
C.2π
$D.2π-\frac {\sqrt {3}-1}{2}$
A
)$A.\frac {2}{3}π-\frac {\sqrt {3}+1}{2}$
$B.\frac {2π}{3}-\frac {\sqrt {3}*1}{2}$
C.2π
$D.2π-\frac {\sqrt {3}-1}{2}$
答案:
A
6. 如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形相邻的两边上.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到点A为止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到点B为止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为 ( )

A.2
B.4 - π
C.π
D.π - 1

A.2
B.4 - π
C.π
D.π - 1
答案:
B 解析:因为四边形ABCD是正方形,所以∠A=∠B=∠C=∠D=90°.当点Q在AB上时,连接BM.因为M为QR的中点,QR=2,所以BM=$\frac{1}{2}$QR=1,即点M的运动轨迹为以点B为圆心,1为半径的$\frac{1}{4}$圆弧.同理,得当点Q 在BC,CD,AD上时,点M的运动轨迹分别为以C,D,A三点为圆心,半径为1的$\frac{1}{4}$圆弧.则线段QR的中点M所经过的路线围成的图形如图中阴影部分所示.所以其面积为2×2−4×$\frac{1}{4}$×π×1²=4−π
B 解析:因为四边形ABCD是正方形,所以∠A=∠B=∠C=∠D=90°.当点Q在AB上时,连接BM.因为M为QR的中点,QR=2,所以BM=$\frac{1}{2}$QR=1,即点M的运动轨迹为以点B为圆心,1为半径的$\frac{1}{4}$圆弧.同理,得当点Q 在BC,CD,AD上时,点M的运动轨迹分别为以C,D,A三点为圆心,半径为1的$\frac{1}{4}$圆弧.则线段QR的中点M所经过的路线围成的图形如图中阴影部分所示.所以其面积为2×2−4×$\frac{1}{4}$×π×1²=4−π

7. 新素养空间观念(2024·黑龙江齐齐哈尔)若圆锥的底面圆半径是1cm,它的侧面展开图的圆心角是直角,则该圆锥的高为
$\sqrt{15}$
cm.
答案:
$\sqrt{15}$
查看更多完整答案,请扫码查看


