《2025年亮点给力大试卷九年级数学上册苏科版》

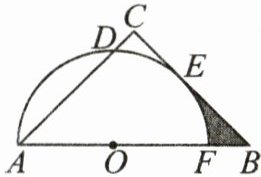
15. (10分)(2023·湖北十堰)如图,在Rt△ABC中,∠C= 90°,AC= BC,点O在AB上,以点O为圆心,OA的长为半径的半圆分别交AC,BC,AB于D,E,F三点,且E是⌢DF的中点.
(1) 求证:直线BC是半圆O的切线;
(2) 若CE= √2,求图中阴影部分的面积(结果保留π).

答案： （1）因为AC=BC,所以∠BAC=∠ABC.又∠C=90°,∠ABC+∠BAC+∠C=180°,所以∠BAC=∠ABC=$\frac{1}{2}$(180°−∠C)=45°.连接OD,OE.因为∠DOF=2∠BAC=90°,且E是⌢DF的中点,所以∠EOF=$\frac{1}{2}$∠DOF=45°.又∠OEC=∠EOF+∠ABC,所以∠OEC=90°,即OE⊥BC.又OE是半圆O的半径,所以直线BC是半圆O的切线.
（2）过点O作OG⊥AD于点G,则∠OGD=∠OGA=90°.由（1）,得OE⊥BC,∠BAC=∠ABC=∠EOF=45°,所以OE=BE.又∠ACB=90°,所以四边形OECG是矩形,即CE=OG.又CE=$\sqrt{2}$,所以OG=$\sqrt{2}$.又∠BAC+∠AOG=90°,所以∠AOG=90°−∠BAC=45°,即∠AOG=∠BAC.所以AG=OG=$\sqrt{2}$.在Rt△AOG中,由勾股定理,得OA=$\sqrt{AG²+OG²}$=2,所以BE=OE=OA=2.又S阴影=S△BOE - S扇形OEF,所以S阴影=$\frac{1}{2}$OE·BE - $\frac{45π×2²}{360}$=2 - $\frac{π}{2}$.

16. (10分)新趋势推导探究回顾旧知:在探究正多边形的有关性质时,我们是从哪几个方面展开的? 探究的方法与过程又是怎样的? (不要求回答)
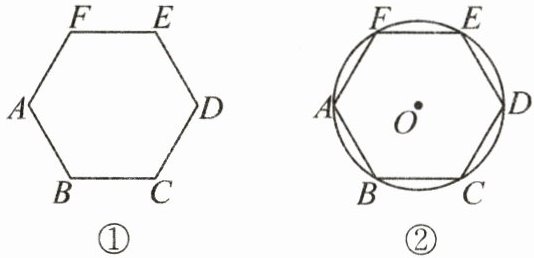
温馨提示:图①是一个边长为a的正六边形.我们知道它具有如下的性质:① 正六边形的每条边的长相等;② 正六边形的六个内角相等,都是120°;③ 正六边形的内角和为720°;④ 正六边形的外角和为360°等.
解答问题:
(1) 观察图②,请你至少写出5条边长为a的正六边形所具有的,且不同于上面的性质;
(2) 尺规作图:在图②中作出圆内接正六边形的内切圆(不要求写作法,只保留作图痕迹);
(3) 求这个正六边形外接圆半径与内切圆半径的比值.

答案：
（1）① 正六边形既是轴对称图形,又是中心对称图形；
② 正六边形的面积为$\frac{3\sqrt{3}}{2}$a²,周长为6a；
③ 正六边形有一个内切圆、一个外接圆,且它们是同心圆；
④ 圆内接正六边形的每条边在圆内所对的优弧的长相等；
⑤ 圆内接正六边形的每条边在圆内所对的优弧的度数相等.（答案不唯一）
（2）圆内接正六边形的内切圆如图：
（3）如图,连接OE,OD.因为多边形ABCDEF为正六边形,所以∠DOE=$\frac{360}{6}$=60°.又OD=OE,ON⊥DE,所以∠EON=$\frac{1}{2}$∠DOE=30°.所以EN=$\frac{1}{2}$OE,即OE=2EN.在Rt△ONE中,由勾股定理,得ON=$\sqrt{OE²-EN²}$=$\sqrt{3}$EN.所以$\frac{OE}{ON}$=$\frac{2EN}{\sqrt{3}EN}$=$\frac{2\sqrt{3}}{3}$.则这个正六边形外接圆半径与内切圆半径的比值为$\frac{2\sqrt{3}}{3}$.

17. (12分)如图①,AB是⊙O的弦,AB= 2,∠AOB= 60°,P是优弧AB上的一个动点(不与A,B两点重合),PA,PB,⌢AB组成了一个新图形(记为“图形P—⌢AB”,即图①中阴影部分).设点P到直线AB的距离为x,图形P—⌢AB的面积为y.
(1) 求y与x之间的函数表达式,并写出自变量x的取值范围;
(2) 记扇形OAB的面积为S_{扇形OAB},且y= S_{扇形OAB}.
① 在图②中,作出一个满足条件的点P(尺规作图,不写作法,保留作图痕迹);
② 在(2)①所作图中,连接PA,PB.再画一条线(包括直线、折线、弧线),将图形P—⌢AB分成面积相等的两部分(画图工具不限,写出必要的文字说明).

答案：
（1）过点O作OC⊥AB于点C,则AC=BC=$\frac{1}{2}$AB.又AB=2,所以AC=BC=1.由题意,得OA=OB,且∠AOB=60°,所以△AOB是等边三角形.所以OA=OB=AB=2.在Rt△AOC中,由勾股定理,得OC=$\sqrt{OA²-AC²}$=$\sqrt{3}$,所以S△AOB=$\frac{1}{2}$AB·OC=$\sqrt{3}$,S扇形OAB=$\frac{60π×2²}{360}$=$\frac{2π}{3}$.又P是优弧AB上的一个动点,所以点P到直线AB的距离最大为OA+OC=2+$\sqrt{3}$.又点P到直线AB的距离为x,所以0＜x≤2+$\sqrt{3}$,S△PAB=$\frac{1}{2}$AB·x=x.所以y=S△PAB + S扇形OAB - S△AOB=x + $\frac{2π}{3}$ - $\sqrt{3}$(0＜x≤2+$\sqrt{3}$).
（2）① 如图①,点P(P₁或P₂)即为所作.
② 以下所有情况都以点P₁为例,点P₂的情况同理即可.第一种,折线的画法(如图②):过点O作ON⊥AB于点N,延长ON交⊙O于点D,连接P₁N,则折线P₁-N-D即为所作;第二种,弧线的画法(如图③):以点P₁为圆心,P₁A的长为半径画弧,交P₁B于点F,则⌢AF即为所作;第三种,直线的画法(如图④):过点O作OG⊥AB于点G,延长OG交⊙O于点H,连接P₁H,过点A作AE//P₁H交BP₁的延长线于点E.取BE的中点M,画直线HM,则直线HM即为所作.