第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
23. (6分)重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装生面(简称“生食”小面).已知3份“堂食”小面和2份“生食”小面的总售价为31元,4份“堂食”小面和1份“生食”小面的总售价为33元.
(1)每份“堂食”小面和“生食”小面的价格分别是多少元?
(2)该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份.为回馈广大食客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格降低$\frac {3}{4}a\%$.统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”小面的销量在4月的基础上增加$\frac {5}{2}a\%$,这两种小面的总销售额在4月的基础上增加$\frac {5}{11}a\%$.求a的值.
(1)每份“堂食”小面和“生食”小面的价格分别是多少元?
(2)该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份.为回馈广大食客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格降低$\frac {3}{4}a\%$.统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”小面的销量在4月的基础上增加$\frac {5}{2}a\%$,这两种小面的总销售额在4月的基础上增加$\frac {5}{11}a\%$.求a的值.
答案:
(1)设每份“堂食”小面价格是的$x$元每份,“生食”小面的价格是$y$元由题意得$\begin{cases}3x+2y=31,\\4x+y=33,\end{cases}$解得$\begin{cases}x=7,\\y=5.\end{cases}$则每份“堂食”小面 的价格7元,每份“生食”小面的价格是5元。
(2)由题意,得$4500×7+2500\cdot\left(1+\frac{5}{2}a\%\right)×5\left(1-\frac{3}{4}a\%\right)=(4500×7+2500×5)\cdot\left(1+\frac{5}{11}a\%\right)$,整理,得$25(a\%)^{2}-2\cdot a\%=0$,解得$a\%=\frac{2}{25}=8\%$或$a\%=0$(舍去).则$a$的值为8.
(1)设每份“堂食”小面价格是的$x$元每份,“生食”小面的价格是$y$元由题意得$\begin{cases}3x+2y=31,\\4x+y=33,\end{cases}$解得$\begin{cases}x=7,\\y=5.\end{cases}$则每份“堂食”小面 的价格7元,每份“生食”小面的价格是5元。
(2)由题意,得$4500×7+2500\cdot\left(1+\frac{5}{2}a\%\right)×5\left(1-\frac{3}{4}a\%\right)=(4500×7+2500×5)\cdot\left(1+\frac{5}{11}a\%\right)$,整理,得$25(a\%)^{2}-2\cdot a\%=0$,解得$a\%=\frac{2}{25}=8\%$或$a\%=0$(舍去).则$a$的值为8.
24. (6分)阅读材料:各类方程的解法.
求解一元一次方程,根据等式的基本性质,把方程转化为$x= a$的形式.求解二元一次方程组,把它转化为一元一次方程来解.类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想——转化,即把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程$x^{3}+x^{2}-2x= 0$,可以通过因式分解把它转化为$x(x^{2}+x-2)= 0$,解方程$x= 0和x^{2}+x-2= 0$,可得方程$x^{3}+x^{2}-2x= 0$的解.
(1)问题:方程$x^{3}+x^{2}-2x= 0的解是x_{1}= 0,x_{2}= $
(2)拓展:用“转化”思想求方程$\sqrt {2x+3}= x$的解;
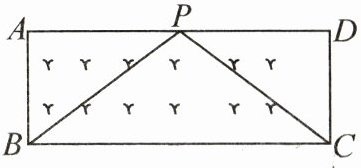
(3)应用:如图,矩形草坪ABCD的长$AD= 8m$,宽$AB= 3m$,小华把一根长为10m的绳子的一端固定在点B,沿草坪边BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边PD,DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
求解一元一次方程,根据等式的基本性质,把方程转化为$x= a$的形式.求解二元一次方程组,把它转化为一元一次方程来解.类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想——转化,即把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程$x^{3}+x^{2}-2x= 0$,可以通过因式分解把它转化为$x(x^{2}+x-2)= 0$,解方程$x= 0和x^{2}+x-2= 0$,可得方程$x^{3}+x^{2}-2x= 0$的解.
(1)问题:方程$x^{3}+x^{2}-2x= 0的解是x_{1}= 0,x_{2}= $
$-2$
,$x_{3}= $1
;(2)拓展:用“转化”思想求方程$\sqrt {2x+3}= x$的解;
方程两边平方得$2x +3=x^{2}$,即$x^{2}-2x-3=0$,解得$x_{1}=3$,$x_{2}=-1$.当$x=-1$时,方程左边$=1$,右边$=-1$,左边$\neq$右边,不符合题意,舍去;当$x=3$时方程左边$=3$,右边$=3$,左边$=$右边,符合题意.则原方程解$x=3$.
(3)应用:如图,矩形草坪ABCD的长$AD= 8m$,宽$AB= 3m$,小华把一根长为10m的绳子的一端固定在点B,沿草坪边BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边PD,DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.

设$AP=x\ \text{m}$.因为四边形$ABCD$是矩形,$AD=8\ \text{m}$,$AB=3\ \text{m}$,所以$\angle A=\angle D=90^{\circ}$,$BC=AD=8\ \text{m}$,$CD=AB=3\ \text{m}$.所以$PD=(8-x)\ \text{m}$.在$\text{Rt}\triangle ABP$和$\text{Rt}\triangle CDP$中,由勾股定理,得$BP=\sqrt{x^{2}+9}\ \text{m}$,$CP=\sqrt{(8-x)^{2}+9}\ \text{m}$.因为$BP+CP=10\ \text{m}$,所以$\sqrt{x^{2}+9}+\sqrt{(8-x)^{2}+9}=10$,即$\sqrt{(8-x)^{2}+9}=10-\sqrt{x^{2}+9}$.两边平方,得$(8-x)^{2}+9=100+x^{2}+9-20\sqrt{x^{2}+9}$.整理,得$5\sqrt{x^{2}+9}=4x+9$.两边平方,得$25(x^{2}+9)=(4x+9)^{2}$.整理,得$x^{2}-8x+16=0$,解得$x_{1}=x_{2}=4$.经检验,$x=4$符合题意.则$AP$的长为$4\ \text{m}$.
答案:
(1)$-2$ 1(或1 $-2$)
(2)方程两边平方得$2x +3=x^{2}$,即$x^{2}-2x-3=0$,解得$x_{1}=3$,$x_{2}=-1$.当$x=-1$时,方程左边$=1$,右边$=-1$,左边$\neq$右边,不符合题意,舍去;当$x=3$时方程左边$=3$,右边$=3$,左边$=$右边,符合题意.则原方程解$x=3$.
(3)设$AP=x\ \text{m}$.因为四边形$ABCD$是矩形,$AD=8\ \text{m}$,$AB=3\ \text{m}$,所以$\angle A=\angle D=90^{\circ}$,$BC=AD=8\ \text{m}$,$CD=AB=3\ \text{m}$.所以$PD=(8-x)\ \text{m}$.在$\text{Rt}\triangle ABP$和$\text{Rt}\triangle CDP$中,由勾股定理,得$BP=\sqrt{x^{2}+9}\ \text{m}$,$CP=\sqrt{(8-x)^{2}+9}\ \text{m}$.因为$BP+CP=10\ \text{m}$,所以$\sqrt{x^{2}+9}+\sqrt{(8-x)^{2}+9}=10$,即$\sqrt{(8-x)^{2}+9}=10-\sqrt{x^{2}+9}$.两边平方,得$(8-x)^{2}+9=100+x^{2}+9-20\sqrt{x^{2}+9}$.整理,得$5\sqrt{x^{2}+9}=4x+9$.两边平方,得$25(x^{2}+9)=(4x+9)^{2}$.整理,得$x^{2}-8x+16=0$,解得$x_{1}=x_{2}=4$.经检验,$x=4$符合题意.则$AP$的长为$4\ \text{m}$.
(1)$-2$ 1(或1 $-2$)
(2)方程两边平方得$2x +3=x^{2}$,即$x^{2}-2x-3=0$,解得$x_{1}=3$,$x_{2}=-1$.当$x=-1$时,方程左边$=1$,右边$=-1$,左边$\neq$右边,不符合题意,舍去;当$x=3$时方程左边$=3$,右边$=3$,左边$=$右边,符合题意.则原方程解$x=3$.
(3)设$AP=x\ \text{m}$.因为四边形$ABCD$是矩形,$AD=8\ \text{m}$,$AB=3\ \text{m}$,所以$\angle A=\angle D=90^{\circ}$,$BC=AD=8\ \text{m}$,$CD=AB=3\ \text{m}$.所以$PD=(8-x)\ \text{m}$.在$\text{Rt}\triangle ABP$和$\text{Rt}\triangle CDP$中,由勾股定理,得$BP=\sqrt{x^{2}+9}\ \text{m}$,$CP=\sqrt{(8-x)^{2}+9}\ \text{m}$.因为$BP+CP=10\ \text{m}$,所以$\sqrt{x^{2}+9}+\sqrt{(8-x)^{2}+9}=10$,即$\sqrt{(8-x)^{2}+9}=10-\sqrt{x^{2}+9}$.两边平方,得$(8-x)^{2}+9=100+x^{2}+9-20\sqrt{x^{2}+9}$.整理,得$5\sqrt{x^{2}+9}=4x+9$.两边平方,得$25(x^{2}+9)=(4x+9)^{2}$.整理,得$x^{2}-8x+16=0$,解得$x_{1}=x_{2}=4$.经检验,$x=4$符合题意.则$AP$的长为$4\ \text{m}$.
查看更多完整答案,请扫码查看


