《2025年亮点给力大试卷九年级数学上册苏科版》

27. (10 分)在如图所示的平面直角坐标系中,O 为原点,$\odot C的圆心坐标为(-2,-2)$,半径为$\sqrt {2}$.直线$y= -x+2$与 x 轴、y 轴分别交于 A,B 两点,点 P 在线段 AB 上运动(包括端点).
(1) 连接 OC,则直线 CO 与 AB 的夹角是90$^{\circ}$;
(2) 当$\triangle POA$是等腰三角形时,求点 P 的坐标;
当△POA为等腰三角形时，有PO=OA 或PO=PA或OA=PA.①当PO=OA时,B,P两点重合，所以点P的坐标为(0,2);②当PO=PA时,因为∠AOB=90°,所以易得P是AB的中点.由(1),得A,B两点的坐标分别为(2,0),(0,2),∠OAB=45°,所以点P的坐标为(1,1);③当PA=OA时,PA=OA=2.过点P作PH⊥OA于点H,连接OP.因为∠PAH=∠OAB=45°,∠PAH+∠APH=90°,所以∠APH=∠PAH=45°,即PH=AH.在Rt△APH中,由勾股定理，得AP²=AH²+PH²,所以2AH²=4,即PH=AH=$\sqrt{2}$(负值已舍去).所以OH=2-$\sqrt{2}$,所以点P的坐标为$(2-\sqrt{2},\sqrt{2})$.综上，点P的坐标为(0,2)或(1,1)或$(2-\sqrt{2},\sqrt{2})$.
(3) 当直线 PO 与$\odot C$相切时,求$∠POA$的度数.
设PO切$\odot C$于点K，连接CK，则CK⊥OK.因为点C的坐标为(-2,-2),所以由勾股定理，得CO=$2\sqrt{2}$.在Rt△COK中,CK=$\sqrt{2}=\frac{1}{2}$CO,所以∠COK=30°.所以∠POD=30°.由(1),得∠AOD=45°.当点K在点C上方时,∠POA=∠AOD-∠POD=15°;当点K在点C下方时,∠POA=∠AOD+∠POD=75°.综上,∠POA的度数为15°或75°.

答案：
(1)90　解析:延长CO与AB交于点D,过点C作CG⊥x轴于点G.因为直线y=-x+2与x轴交于点A，与y轴交于点B,所以易得点A的坐标为(2,0),点B的坐标为(0,2),即OA=OB=2.又∠AOB=90°,所以△AOB是等腰直角三角形,即∠DAO=∠OAB=45°.因为点C的坐标为(-2,-2),所以CG=OG=2.所以△OCG是等腰直角三角形,即∠COG=45°.所以∠AOD=45°.又∠AOD+∠ODA+∠DAO=180°,所以∠ODA=90°.则直线CO与AB的夹角是90°.
(2)当△POA为等腰三角形时，有PO=OA 或PO=PA或OA=PA.①当PO=OA时,B,P两点重合，所以点P的坐标为(0,2);②当PO=PA时,因为∠AOB=90°,所以易得P是AB的中点.由
(1),得A,B两点的坐标分别为(2,0),(0,2),∠OAB=45°,所以点P的坐标为(1,1);③当PA=OA时,PA=OA=2.过点P作PH⊥OA于点H,连接OP.因为∠PAH=∠OAB=45°,∠PAH+∠APH=90°,所以∠APH=∠PAH=45°,即PH=AH.在Rt△APH中,由勾股定理，得AP²=AH²+PH²,所以2AH²=4,即PH=AH=$\sqrt{2}$(负值已舍去).所以OH=2-$\sqrt{2}$,所以点P的坐标为$(2-\sqrt{2},\sqrt{2})$.综上，点P的坐标为(0,2)或(1,1)或$(2-\sqrt{2},\sqrt{2})$.
(3)设PO切⊙O于点K，连接CK，则CK⊥OK.因为点C的坐标为(-2,-2),所以由勾股定理，得CO=$2\sqrt{2}$.在Rt△COK中,CK=$\sqrt{2}=\frac{1}{2}$CO,所以∠COK=30°.所以∠POD=30°.由
(1),得∠AOD=45°.当点K在点C上方时,∠POA=∠AOD-∠POD=15°;当点K在点C下方时,∠POA=∠AOD+∠POD=75°.综上,∠POA的度数为15°或75°.

28. (10 分)【问题提出】
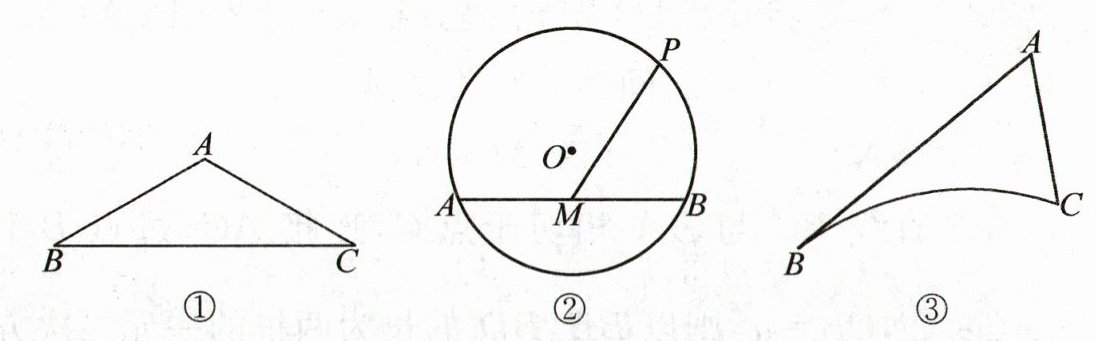
(1) 如图①,在$\triangle ABC$中,$∠A= 120^{\circ},AB= AC= 5$,则$\triangle ABC$的外接圆半径 R 的值为______;
【问题探究】
(2) 如图②,$\odot O$的半径为 13,弦$AB= 24$,M 是 AB 的中点,P 是$\odot O$上的一动点,求 PM 的长的最大值;
【问题解决】
(3) 如图③,AB,AC,$\overset{\frown}{BC}$是某新区的三条规划路,其中$AB= 6km,AC= 3km,∠BAC= 60^{\circ}$,$\overset{\frown}{BC}所对的圆心角为60^{\circ}$. 新区管委会想在$\overset{\frown}{BC}$路边建物资总站点 P,在 AB,AC 路边分别建物资分站点 E,F,也就是分别在$\overset{\frown}{BC}$、线段 AB 和 AC 上选取 P,E,F 三点. 由于总站工作人员每天要将物资在各物资站点间按$P→E→F→P$的路径进行运输,因此,要在各物资站点之间规划道路 PE、EF 和 FP. 为了快捷、环保和节约成本,要使线段 PE,EF,FP 的长度之和最短,试求$PE+EF+FP$的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).

答案：

(1)5　解析:过点A作AD⊥BC于点D.因为AB=AC=5,所以∠B=∠C.又∠B+∠C+∠BAC=180°,∠BAC=120°,所以∠B=$\frac{1}{2}(180^{\circ}-\angle BAC)=30^{\circ}$.所以AD=$\frac{1}{2}AB=\frac{5}{2}$.在Rt△ABD中,由勾股定理，得BD=$\sqrt{AB^{2}-AD^{2}}=\frac{5\sqrt{3}}{2}$.设△ABC的外接圆的圆心为O,连接OA,OB.由题意,得点D在OA上,则OA=OB=R.所以OD=OA-AD=$R-\frac{5}{2}$.在Rt△OBD中,由勾股定理,得OB²=OD²+BD²,所以$R^{2}=(R-\frac{5}{2})^{2}+(\frac{5\sqrt{3}}{2})^{2}$,解得R=5.则R的值为5.
(2)如图①,连接MO并延长,与⊙O相交于点P',连接OA,OB,OP.因为M是AB的中点,OA=OB=13,AB=24,所以MO⊥AB,AM=$\frac{1}{2}AB=12$.在Rt△AOM中,由勾股定理,得OM=$\sqrt{OA^{2}-AM^{2}}=5$.因为PM≤OM+OP=OM+OP'=MP'=18,所以当点P运动到点P'时,PM的长取最大值，且最大值为18.
(3)如图②,P'为$\overset{\frown}{BC}$上任意一点，分别作点P'关于直线AB,AC的对称点P'₁,P'₂,连接P'₁P'₂,分别与AB,AC相交于E',F'两点,连接P'E',P'F',所以△P'Eid:31
content:28. (10 分)【问题提出】
(1) 如图①,在$\triangle ABC$中,$∠A= 120^{\circ},AB= AC= 5$,则$\triangle ABC$的外接圆半径 R 的值为______;
【问题探究】
(2) 如图②,$\odot O$的半径为 13,弦$AB= 24$,M 是 AB 的中点,P 是$\odot O$上的一动点,求 PM 的长的最大值;
【问题解决】
(3) 如图③,AB,AC,$\overset{\frown}{BC}$是某新区的三条规划路,其中$AB= 6km,AC= 3km,∠BAC= 60^{\circ}$,$\overset{\frown}{BC}所对的圆心角为60^{\circ}$. 新区管委会想在$\overset{\frown}{BC}$路边建物资总站点 P,在 AB,AC 路边分别建物资分站点 E,F,也就是分别在$\overset{\frown}{BC}$、线段 AB 和 AC 上选取 P,E,F 三点. 由于总站工作人员每天要将物资在各物资站点间按$P→E→F→P$的路径进行运输,因此,要在各物资站点之间规划道路 PE、EF 和 FP. 为了快捷、环保和节约成本,要使线段 PE,EF,FP 的长度之和最短,试求$PE+EF+FP$的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).

answer:
(1)5　解析:过点A作AD⊥BC于点D.因为AB=AC=5,所以∠B=∠C.又∠B+∠C+∠BAC=180°,∠BAC=120°,所以∠B=$\frac{1}{2}(180^{\circ}-\angle BAC)=30^{\circ}$.所以AD=$\frac{1}{2}AB=\frac{5}{2}$.在Rt△ABD中,由勾股定理，得BD=$\sqrt{AB^{2}-AD^{2}}=\frac{5\sqrt{3}}{2}$.设△ABC的外接圆的圆心为O,连接OA,OB.由题意,得点D在OA上,则OA=OB=R.所以OD=OA-AD=$R-\frac{5}{2}$.在Rt△OBD中,由勾股定理,得OB²=OD²+BD²,所以$R^{2}=(R-\frac{5}{2})^{2}+(\frac{5\sqrt{3}}{2})^{2}$,解得R=5.则R的值为5.
(2)如图①,连接MO并延长,与⊙O相交于点P',连接OA,OB,OP.因为M是AB的中点,OA=OB=13,AB=24,所以MO⊥AB,AM=$\frac{1}{2}AB=12$.在Rt△AOM中,由勾股定理,得OM=$\sqrt{OA^{2}-AM^{2}}=5$.因为PM≤OM+OP=OM+OP'=MP'=18,所以当点P运动到点P'时,PM的长取最大值，且最大值为18.
(3)如图②,P'为$\overset{\frown}{BC}$上任意一点，分别作点P'关于直线AB,AC的对称点P'₁,P'₂,连接P'₁P'₂,分别与AB,AC相交于E',F'两点,连接P'E',P'F',所以△P'E'F'的周长=P'E'+E'F'+P'F'=P'₁E'+E'F'+P'₂F'=P'₁P'₂,对于点P'及分别在AB,AC上的任意两点E,F，有△P'EF的周长≥△P'E'F'的周长=P'₁P'₂,即△P'EF周长的最小值为P'₁P'₂的长.连接AP'₁,AP',AP'₂,则AP'₁=AP'=AP'₂,∠P'₁AB=∠P'AB,∠P'₂AC=∠P'AC.所以∠P'₁AP'₂=2∠BAC.又∠BAC=60°,所以∠P'₁AP'₂=120°.同
(1),易得P'₁P'₂=$\sqrt{3}$AP'₁=$\sqrt{3}$AP'.所以要使P'₁P'₂最短,只要AP'最短.设O为$\overset{\frown}{BC}$所在圆的圆心,连接OB,OC,OP',OA，且OA与$\overset{\frown}{BC}$相交于点P,则AP'+P'O≥AO.所以AP'≥AP.则当点P'为点P时,AP'最短,即P'₁P'₂最短.连接BC,易证△ACB为直角三角形，且∠ABC=30°,∠ACB=90°.在Rt△ABC中,AB=6km,AC=3km,由勾股定理,得BC=$\sqrt{AB^{2}-AC^{2}}=3\sqrt{3}$km.因为∠BOC=60°,OB=OC,所以△BOC是等边三角形,即BO=BC=$3\sqrt{3}$km,∠OBC=60°.所以∠ABO=∠ABC+∠OBC=90°.在Rt△ABO中,由勾股定理，得AO=$\sqrt{AB^{2}+BO^{2}}=3\sqrt{7}$km.所以$\sqrt{3}$AP'=$\sqrt{3}$AP=$\sqrt{3}(AO-OP)=\sqrt{3}(AO-BO)=(3\sqrt{21}-9)$km.所以P'₁P'₂的长的最小值为$\sqrt{3}AP'=(3\sqrt{21}-9)$km.所以PE+EF+FP 的最小值为$(3\sqrt{21}-9)$km.