《2025年启东中学作业本九年级数学上册人教版》

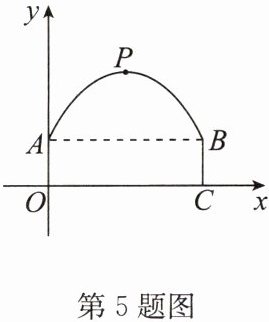
5. (2024·高港区期末)一条隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.
(1)求抛物线的函数解析式;
(2)该隧道内设双行道,中间隔离带宽1m,一辆货车高4m,宽2.5m,能否安全通过?为什么?

答案： 解:
(1)设抛物线的函数解析式为$y=a(x-h)^2+k$,
由题意知顶点为(4,6),
∴$y=a(x-4)^2+6$,
∵抛物线过点(0,2),
∴$a(0-4)^2+6=2$,解得$a=-\frac{1}{4}$,
∴抛物线的函数解析式为$y=-\frac{1}{4}(x-4)^2+6$.
(2)不能.理由:$(8-1)÷2=3.5(m)$,3.5-2.5=1(m).
当x=1时,$y=\frac{15}{4}＜4$,
∴该货车不能安全通过隧道.

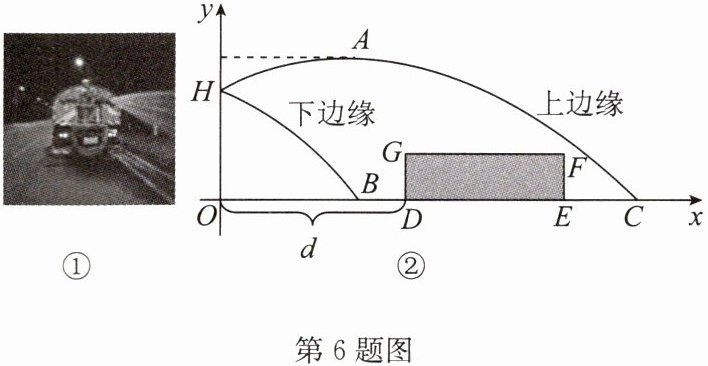
6. (2024·江都区期末)如图①是洒水车为绿化带浇水的场景.洒水车喷水口H离地竖直高度OH为1.2m,喷出的水的上、下边缘近似地看作两条抛物线,下边缘抛物线是由上边缘抛物线向左平移得到的,上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.4m.把绿化带横截面抽象为矩形DEFG,绿化带的水平宽度$DE = 3m$,竖直高度$EF = 0.6m$.洒水车到绿化带的距离OD为d(单位:m),建立如图②所示的平面直角坐标系.
(1)若距喷水口水平距离为5.5米的地方正好有一个行人经过,试判断该行人是否会被洒水车淋到水?并写出你的判断过程;
(2)要使洒水车行驶时喷出的水能浇灌到整个绿化带,则洒水车离绿化带的距离d的范围是多少?

答案： 解:
(1)设上边缘抛物线的函数解析式为$y_1=a(x-h)^2+k$.
由题意可得,h=2,k=1.6,
∴$y_1=a(x-2)^2+1.6$.
∵H(0,1.2),
∴$1.2=a(0-2)^2+1.6$.
∴a=-0.1.
∴$y_1=-0.1(x-2)^2+1.6$.
当$y_1=0$时,x=6或x=-2(舍去).
∵6＞5.5,
∴行人会被洒水车淋到水.
(2)将y=0.6代入$y=-\frac{1}{10}(x-2)^2+1.6$得
$0.6=-\frac{1}{10}(x-2)^2+1.6$,整理得,$(x-2)^2=10$,
解得$x=2+\sqrt{10}$或$x=2-\sqrt{10}$(舍去).
∵当x＞2时,y随x的增大而减小,
∴当2≤x≤6时,要使y≥0.6,则$x\leq2+\sqrt{10}$.
∴$d\leq2+\sqrt{10}-3=\sqrt{10}-1$.
∵H(0,1.2)关于直线x=2的对称点为(4,1.2),
∴下边缘抛物线是由上边缘抛物线向左平移4 m得到的.
∴B(2,0).由下边缘抛物线可得,d≥OB=2.
综上所述,$2\leq d\leq\sqrt{10}-1$.