《2025年启东中学作业本九年级数学上册人教版》

6. 飞机着陆后滑行的距离 y(单位:m)关于滑行时间 t(单位:s)的函数解析式是$y= 60t-\frac {3}{2}t^{2}$,在飞机着陆滑行中,最后 4 s 滑行的距离是24m.

答案： 24

7. (2024·宁津期末)如图,现打算用 60 m 的篱笆围成一个“日”字形菜园 ABCD(含隔离栏 EF),菜园的一面靠墙 MN,墙 MN 可利用的长度为 39 m.(篱笆的宽度忽略不计)
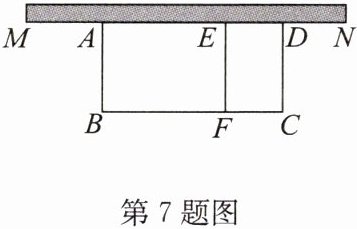
(1)菜园面积可能为$252m^{2}$吗? 若可能,求 AB 的长;若不可能,请说明理由.
(2)因场地限制,菜园的宽度 AB 不能超过 8 m,求该菜园面积的最大值.

答案： 解:
(1)设 AB 的长为x m,则 BC 的长为$(60-3x)m.$
根据题意得$x(60-3x)=252$,解得$x=6$或$x=14,$
当$x=6$时,$BC=60-18=42＞39$,舍去;
当$x=14$时,$BC=60-42=18＜39$,满足题意,
∴菜园的面积可能是$252m^{2}$,此时 AB 的长为14 m.
(2)设 AB 的长为x m,菜园的面积为$y{m}^{2}$,由题意得
$y=x(60-3x)=-3x^{2}+60x=-3(x-10)^{2}+300.$
$\because -3＜0$,
∴当$x＜10$时,y随x的增大而增大,
$\because x≤8$,
∴当$x=8$时,y最大,最大值为288.
答:该菜园面积的最大值为$288m^{2}.$

8. (2023·海门区模拟)某建筑工程队借助一段废弃的墙体 CD(CD 长为 18 米),用 76 米长的铁栅栏围成两个相连的长方形仓库,为了方便取物,在两个仓库之间留出了 1 米宽的缺口作通道,在平行于墙的一边留下一个 1 米宽的缺口作小门. 现有如图所示的两种设计方案(图①点 A 在线段 DC 的延长线上,图②点 A 在线段 DC 上),设$AB= x$米,图①,图②中仓库的总面积分别为$y_{1}$平方米,$y_{2}$平方米.
(1)分别写出$y_{1},y_{2}$与x的函数关系式;
(2)小红说:“$y_{1}$的最大值为 384,$y_{2}$的最大值为 507. ”你同意吗? 请说明理由.

答案： 解:
(1)题图①中,$AD=\frac {76+18+1-(3x-1)}{2}=\frac {96-3x}{2},$
$\therefore y_{1}=AB\cdot AD=x\cdot \frac {96-3x}{2}=-\frac {3}{2}x^{2}+48x.$
题图②中,$AD=76+1-(3x-1)=78-3x,$
$\therefore y_{2}=AB\cdot AD=x\cdot (78-3x)=-3x^{2}+78x.$
(2)不同意小红的说法,理由:
$y_{1}=-\frac {3}{2}x^{2}+48x=-\frac {3}{2}(x^{2}-32x)=-\frac {3}{2}(x^{2}-$
$32x+256-256)=-\frac {3}{2}[(x-16)^{2}-256]=-\frac {3}{2}(x-$
$16)^{2}+384.$
$\because -\frac {3}{2}＜0$,
∴$y_{1}$有最大值,
当$x=16$时,$AD=\frac {96-3x}{2}=24$,符合题意,此时$y_{1}$有最大值,是384.
$y_{2}=-3x^{2}+78x=-3(x^{2}-26x)=-3(x^{2}-26x+$
$169-169)=-3[(x-13)^{2}-169]=-3(x-13)^{2}+507,$
$\because -3＜0$,
∴当$x=13$时,$y_{2}$有最大值,是507,
当$x=13$时,$AD=78-3x=78-39=39＞18$,不符合题意,
$\therefore y_{2}$的最大值不能是507,
∴不同意小红的说法.