第110页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1.(2024·泸州)如图,EA,ED 是$\odot O$的切线,切点分别为 A,D,点 B,C 在$\odot O$上.若$∠BAE+∠BCD= 236^{\circ }$,则$∠E$的大小为(
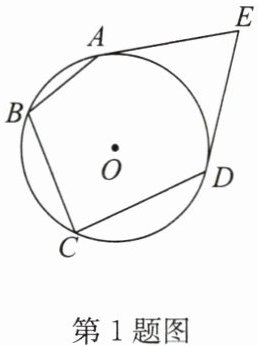
A.$56^{\circ }$
B.$60^{\circ }$
C.$68^{\circ }$
D.$70^{\circ }$
C
)
A.$56^{\circ }$
B.$60^{\circ }$
C.$68^{\circ }$
D.$70^{\circ }$
答案:
C
2.(2024·东城区期末)如图,$\odot O是\triangle ABC$的内切圆,与 AB,BC,AC 分别相切于点 D,E,F.若$\odot O$的半径为 2,$AB= 6,AC= 8,BC= 12$,则$\triangle ABC$的面积为(
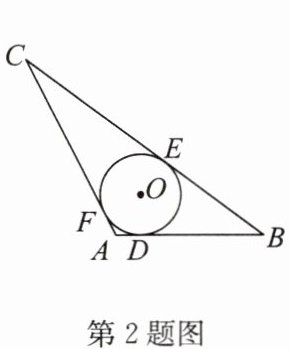
A.$12\sqrt {3}$
B.24
C.26
D.52
C
)
A.$12\sqrt {3}$
B.24
C.26
D.52
答案:
C
3.数学文化(2024·北仓期末)《九章算术》是我国古代数学的瑰宝,其中有著名的“勾股容圆”问题,原文为:“今有勾八步,股一十五步.问勾中容圆径几何?”意思是“今有直角三角形,较短直角边长 8 步,较长直角边长 15 步,问此直角三角形内切圆的直径是多少步?”我们用学过的知识可求该内切圆的直径是
6
步.
答案:
6
4.(2024·昆山期末)如图,$\triangle ABC$的周长是 18 cm,点 O 是$\triangle ABC$的内心,过点 O 作$EF// AB$,与 AC,BC 分别交于点 E,F.已知$AB= 6cm$,则$\triangle CEF$的周长为
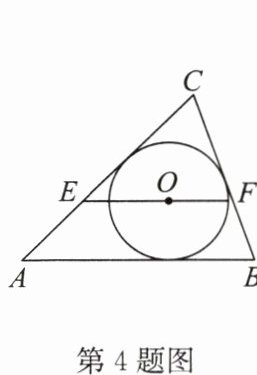
12
cm.
答案:
12
5.如图,以正方形 ABCD 的 AB 边为直径作半圆 O,过点 C 作直线切半圆 O 于点 F,交 AD 边于点 E.若$\triangle CDE$的周长为 12,则直角梯形 ABCE 的周长为
14
.
答案:
14
6.如图,$\triangle ABC的内切圆\odot O$与 BC,CA,AB 分别相切于点 D,E,F,且$AB= 18cm,BC= 28cm,CA= 26cm$,求 AF,BD,CE 的长.


答案:
解:由切线长定理得AF=AE,BF=BD,CD=CE.
设AF=AE=x cm,则BF=BD=(18-x)cm,CD=CE=(10+x)cm.
∵AE+EC=26 cm,
∴x+10+x=26,解得x=8.
∴AF=8 cm,BD=18-x=18-8=10(cm),CE=10+x=10+8=18(cm).
设AF=AE=x cm,则BF=BD=(18-x)cm,CD=CE=(10+x)cm.
∵AE+EC=26 cm,
∴x+10+x=26,解得x=8.
∴AF=8 cm,BD=18-x=18-8=10(cm),CE=10+x=10+8=18(cm).
7.如图,$\odot I是\triangle ABC$的内切圆,D,E,F 为三个切点.若$∠DEF= 52^{\circ }$,则$∠A$的度数为(

A.$76^{\circ }$
B.$68^{\circ }$
C.$52^{\circ }$
D.$38^{\circ }$
A
)
A.$76^{\circ }$
B.$68^{\circ }$
C.$52^{\circ }$
D.$38^{\circ }$
答案:
A
查看更多完整答案,请扫码查看


