《2025年启东中学作业本九年级数学上册人教版》

8. (2024·武汉期末)如图,直线 EF 与$\odot O$相切于点 C,直线 EO 与$\odot O$相交于点 D,连接 CD. 若$∠DEF= 3∠D$,则$∠DCF$的度数为____$72^{\circ }$.

答案： $72^{\circ }$

9. (2024·包头)如图,四边形 ABCD 是$\odot O$的内接四边形,点 O 在四边形 ABCD 内部,过点 C 作$\odot O$的切线交 AB 的延长线于点 P,连接 OA,OB. 若$∠AOB= 140^{\circ },∠BCP= 35^{\circ }$,则$∠ADC$的度数为$105^{\circ }$.

答案： $105^{\circ }$

10. (2024·房山区期末)在平面直角坐标系 xOy 中,A 为 y 轴正半轴上一点,点 B(1,0),C(5,0),$\odot P是\triangle ABC$的外接圆. 当$∠BAC$最大时,点 A 的坐标为$(0,\sqrt{5})$.

答案： $(0,\sqrt{5})$

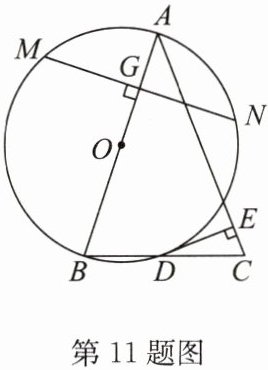
11. (2024·雨花区期末)如图,在$\triangle ABC$中,$AB= AC$,以 AB 为直径的$\odot O$与 BC 相交于点 D,$DE⊥AC$,垂足为 E.
(1)求证:DE 是$\odot O$的切线;
(2)若弦 MN 垂直于 AB,垂足为 G,$\frac {AG}{AB}= \frac {1}{4},MN= \sqrt {2}$,求$\odot O$的直径.

答案：

(1)证明:如答图①,连接OD,
　
∵OB=OD,
∴∠OBD=∠ODB.
　
∵AB=AC,
∴∠ABC=∠ACB,
　
∴∠ODB=∠ACB,
∴OD//AC;
　
∵DE⊥AC,
∴DE⊥OD.
　
∵OD是⊙O的半径，
∴DE是⊙O的切线.
　　
(2)解:如答图②,连接OM.
　
∵AB⊥MN,且AB为⊙O的直径,MN=$\sqrt{2}$,
　
∴$MG=\frac{1}{2}MN=\frac{\sqrt{2}}{2}$.
　设⊙O的半径为r,则OM=r,AB=2r.
　
∵$\frac{AG}{AB}=\frac{1}{4}$,
∴$AG=\frac{1}{4}AB=\frac{1}{2}r$,
　
∴$OG=OA−AG=\frac{1}{2}r$.
在Rt△OGM中,根据勾股定理,得$OG^{2}+MG^{2}=OM^{2}$,即$(\frac{1}{2}r)^{2}+(\frac{\sqrt{2}}{2})^{2}=r^{2}$,
　解得$r=\frac{\sqrt{6}}{3}$,
∴$AB=\frac{2\sqrt{6}}{3}$.
　即⊙O的直径为$\frac{2\sqrt{6}}{3}$.

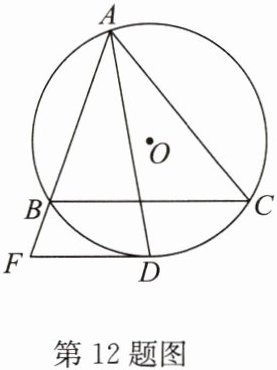
12. (2024·德阳)如图,已知$\odot O$的半径为 5,B,C 是$\odot O$上两定点,A 是$\odot O$上一动点,且$∠BAC= 60^{\circ },∠BAC的平分线交\odot O$于点 D.
(1)求证:D 为$\widehat {BC}$上一定点.
(2)过点 D 作 BC 的平行线交 AB 的延长线于点 F.
①判断 DF 与$\odot O$的位置关系,并说明理由;
②若$\triangle ABC$为锐角三角形,求 DF 的取值范围.

答案：

(1)证明:连接OB,OD,如答图①.
∵∠BAC=$60^{\circ }$,∠BAC的平分线交⊙O于点D,
∴∠BAD=$\frac{1}{2}$∠BAC=30°,
∴∠BOD=2∠BAD=60°,
∴$\overset{\frown }{BD}$的度数是$60^{\circ }$.
∵B为定点,
∴D为$\overset{\frown }{BC}$上一定点.
(2)解:①DF与⊙O相切.理由如下:
　连接OD,如答图②.
∵∠BAC的平分线交⊙O于点D,
∴∠BAD=∠CAD,
∴$\overset{\frown }{BD}=\overset{\frown }{CD}$,
∴OD⊥BC.
∵DF//BC,
∴OD⊥DF.
∵OD为⊙O的半径，
∴DF与⊙O相切.
　②当∠$A_{1}$BC为直角时，连接OD交BC于点M,如答图③.
∵∠$BA_{1}C$=60°,∠$A_{1}BC$=90°,
∴∠C=30°,$A_{1}C$为⊙O的直径,
∵⊙O的半径为5,
∴$A_{1}C$=10,$A_{1}B$=$\frac{1}{2}$$A_{1}C$=5,
∴$BC=5\sqrt{3}$,由①知,$\overset{\frown }{BD}=\overset{\frown }{CD}$,
∴$BM=\frac{1}{2}BC=\frac{5\sqrt{3}}{2}$,∠BMD=90°.
∵∠FBC=180°−∠$A_{1}BC$=90°,∠FDM=90°,
∴四边形BFDM是矩形,
∴$DF=BM=\frac{5\sqrt{3}}{2}$;
　当∠$A_{2}CB$为直角时，连接OD,BD,如答图④.
∵∠$A_{2}CB$=90°,∠$BA_{2}C$=60°,
∴$A_{2}B$是⊙O的直径,∠$A_{2}BC$=30°.
∵DF//BC,
∴∠F=∠$A_{2}BC$=30°.
∵DF与⊙O相切,
∴∠FDO=90°,
∴OF=2OD=10,
∴$DF=\sqrt{OF^{2}-OD^{2}}=\sqrt{10^{2}-5^{2}}=5\sqrt{3}$.
　由图可知，当点A由点$A_{1}$运动到点$A_{2}$(不包括点$A_{1}$，点$A_{2}$)时，△ABC是锐角三角形,
∴DF的取值范围是$\frac{5\sqrt{3}}{2}$＜DF＜$5\sqrt{3}$