第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
6.数学文化(2024·南昌期末)欧几里得在《几何原本》中,记载了用图解法解方程$x^{2}+ax= b^{2}$的方法,类似地,我们可以用折纸的方法求方程$x^{2}+2x-4= 0$的一个正根. 如图,一张边长为 2的正方形纸片 ABCD,先折出 AB,CD 的中点 E,F,再沿过点 B 的直线折叠,使点 A 落在线段 BF 上(即点 H 处),折痕为 BG,点 G 在边 AD 上,连接 GH,GF,其长度恰好是方程$x^{2}+2x-4= 0$的一个正根的线段为 (
A.GA
B.GD
C.GF
D.FC
A
)A.GA
B.GD
C.GF
D.FC
答案:
A
7.数学文化(2024·南通通州期末)《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何. 意思是:一根竿子横放,竿比门宽长出四尺;竖放,竿比门高长出二尺,斜放恰好能出去,则竿长为 (
A.10 尺
B.5 尺
C.10 尺或 2 尺
D.5 尺或 4 尺
A
)A.10 尺
B.5 尺
C.10 尺或 2 尺
D.5 尺或 4 尺
答案:
A
8.如图,在矩形 ABCD 中,$AB= 10cm,AD= 8cm$,点 P 从点 A 出发沿 AB 以 2 cm/s 的速度向点 B 运动,同时点 Q 从点 B 出发沿 BC 以 1 cm/s 的速度向点 C 运动,点 P 到达终点后,P,Q两点同时停止运动,则
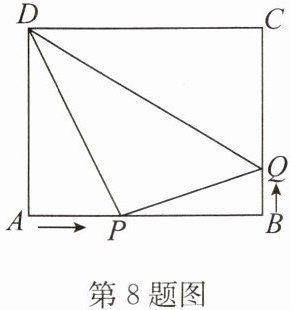
2或3
s时,$△BPQ的面积是6cm^{2}$.
答案:
2或3
9.(2024·海门期末)如图,有一块矩形铁皮,长 100 cm,宽 50 cm,在它的四个角各切去一个同样大小的正方形,然后将四周突出的部分折起,就能制作一个无盖方盒. 如果制作的无盖方盒的底面积为$3600cm^{2}$,那么矩形铁皮各角应该切去的正方形的边长是多少?
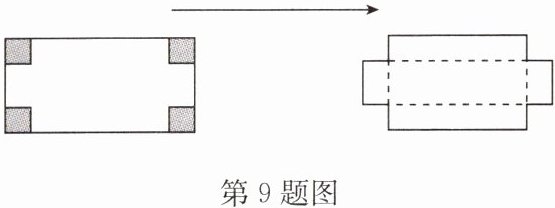

答案:
解:设切去的正方形的边长为$x\ \text{cm}$,则盒子底的长为$(100-2x)\ \text{cm}$,宽为$(50-2x)\ \text{cm}$.根据题意得$(100-2x)(50-2x)=3600$,整理得$x^{2}-75x+350=0$,解得$x_{1}=5$,$x_{2}=70$.$\because$当$x=70$时,$50-2x<0$,不合题意舍去,$\therefore x=5$.答:切去的正方形的边长为5 cm.
10.(2023 春·如皋期末)某学校在“美化校园,幸福学习”活动中,计划利用如图所示的直角墙角(阴影部分,两边足够长),用 20 m 长的篱笆围成一个矩形花园 ABCD(篱笆只围 AB,AD 两边).
(1)若花园的面积为$75m^{2}$,求 AB 的长.
(2)若在直角墙角内点 P 处有一棵桂花树,且到墙 CD 的距离为 12 m,若要将这棵树围在矩形花园内(含边界,不考虑树的粗细),问该花园的面积能否为$100m^{2}$? 若能,求出 AB 的长;若不能,请说明理由.
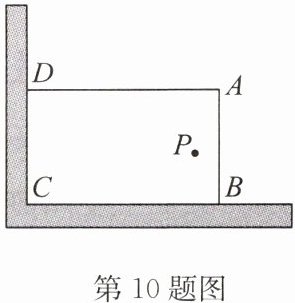
(1)若花园的面积为$75m^{2}$,求 AB 的长.
(2)若在直角墙角内点 P 处有一棵桂花树,且到墙 CD 的距离为 12 m,若要将这棵树围在矩形花园内(含边界,不考虑树的粗细),问该花园的面积能否为$100m^{2}$? 若能,求出 AB 的长;若不能,请说明理由.

答案:
解:
(1)设$AB=x\ \text{m}$,根据题意,得$x(20-x)=75$,解得$x_{1}=5$,$x_{2}=15$.答:AB的长为5 m或15 m.
(2)将这棵树围在矩形花园内,面积不能为$100\ \text{m}^{2}$.设AD的长为$y\ \text{m}$,则$y(20-y)=100$,解得$y=10$,$\because 10<12$,
∴将这棵树围在矩形花园内,面积不能为$100\ \text{m}^{2}$.
(1)设$AB=x\ \text{m}$,根据题意,得$x(20-x)=75$,解得$x_{1}=5$,$x_{2}=15$.答:AB的长为5 m或15 m.
(2)将这棵树围在矩形花园内,面积不能为$100\ \text{m}^{2}$.设AD的长为$y\ \text{m}$,则$y(20-y)=100$,解得$y=10$,$\because 10<12$,
∴将这棵树围在矩形花园内,面积不能为$100\ \text{m}^{2}$.
查看更多完整答案,请扫码查看


