《2025年全效学习学业评价方案九年级数学上册北师大版》

2. 一般认为,如果一个人的肚脐以上的高度(上半身)与肚脐以下的高度(下半身)符合黄金分割,则这个人更好看.一位参加空姐选拔活动的选手,她的上半身长65cm,下半身长95cm,那么她穿多高的鞋子才能更好看？(结果精确到1cm;参考数据:黄金分割比为$\frac {\sqrt {5}-1}{2},\sqrt {5}\approx 2.236)$

答案： 解：设她穿$x cm$高的鞋子才能更好看。
根据黄金分割的定义，可得$\frac{65}{95 + x}=\frac{\sqrt{5}-1}{2}$。
将$\sqrt{5}\approx2.236$代入上式：
$\begin{aligned}\frac{65}{95 + x}&=\frac{2.236 - 1}{2}\\frac{65}{95 + x}&=\frac{1.236}{2}\\1.236×(95 + x)&=65×2\\1.236×95+1.236x&=130\\117.42+1.236x&=130\\1.236x&=130 - 117.42\\1.236x&=12.58\\x&=\frac{12.58}{1.236}\\x&\approx10\end{aligned}$
所以她穿$10cm$高的鞋子才能更好看。

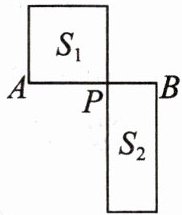
3. 如图,已知点P是线段AB的黄金分割点,且$PA＞PB$.若$S_{1}$表示以PA为一边的正方形的面积,$S_{2}$表示长是AB、宽是PB的矩形的面积,则$S_{1}$=$S_{2}$(填“＞”“＜”或“=”).

答案： $=$

4. 如图,在$△ABC$中,点D是线段AC的黄金分割点,且$AD＜CD,AB=CD.$
(1)求证:$∠ABC=∠ADB;$
(2)若$BC=4cm$,求BD的长.$(2\sqrt{5}-2)cm$

答案： 1. （1）证明：
因为点$D$是线段$AC$的黄金分割点，且$AD\lt CD$，所以$CD^{2}=AD\cdot AC$。
又因为$AB = CD$，所以$AB^{2}=AD\cdot AC$，即$\frac{AB}{AD}=\frac{AC}{AB}$。
在$\triangle ABC$和$\triangle ADB$中，$\frac{AB}{AD}=\frac{AC}{AB}$，$\angle A=\angle A$（公共角）。
根据相似三角形的判定定理（两边对应成比例且夹角相等的两个三角形相似），可得$\triangle ABC\sim\triangle ADB$。
由相似三角形的性质（相似三角形对应角相等），所以$\angle ABC=\angle ADB$。
2. （2）解：
因为$\triangle ABC\sim\triangle ADB$，所以$\frac{BC}{BD}=\frac{AC}{AB}$，又$AB = CD$，$CD^{2}=AD\cdot AC$，$\frac{AB}{AD}=\frac{AC}{AB}$，且$\triangle ABC\sim\triangle ADB$，则$\frac{BC}{BD}=\frac{AB}{AD}$。
因为$\triangle ABC\sim\triangle ADB$，所以$\frac{BD}{AB}=\frac{AB}{AC}$，又$AB = CD$，$CD^{2}=AD\cdot AC$，设$BD = x$。
由$\triangle ABC\sim\triangle ADB$可得$\frac{BC}{BD}=\frac{AB}{AD}$，且$AB^{2}=AD\cdot AC$，$\triangle ABC\sim\triangle ADB$，所以$BD^{2}=AD\cdot AB$，$BC^{2}=AB\cdot AC$。
因为$\triangle ABC\sim\triangle ADB$，所以$\frac{BD}{BC}=\frac{AD}{AB}$，又$AB^{2}=AD\cdot AC$，$\frac{AB}{AC}=\frac{AD}{AB}$，由$\triangle ABC\sim\triangle ADB$得$\frac{BD}{BC}=\frac{AB}{AC}$，且$AB = CD$，$CD^{2}=AD\cdot AC$，$\frac{CD}{AC}=\frac{\sqrt{5}-1}{2}$（黄金分割比例）。
因为$\triangle ABC\sim\triangle ADB$，所以$\frac{BD}{BC}=\frac{AD}{AB}$，$AB^{2}=AD\cdot AC$，$\frac{AB}{AC}=\frac{AD}{AB}$，$\triangle ABC\sim\triangle ADB$，则$BD^{2}=BC\cdot AD$，$AB^{2}=AD\cdot AC$，$\frac{AB}{AC}=\frac{AD}{AB}$。
由$\triangle ABC\sim\triangle ADB$，根据相似三角形对应边成比例$\frac{BD}{AB}=\frac{AB}{AC}$，又$AB = CD$，$CD^{2}=AD\cdot AC$，$\frac{CD}{AC}=\frac{\sqrt{5}-1}{2}$，且$\triangle ABC\sim\triangle ADB$，$\frac{BD}{BC}=\frac{\sqrt{5}-1}{2}$。
已知$BC = 4cm$，因为$\triangle ABC\sim\triangle ADB$，所以$BD^{2}=BC\cdot AD$，$AB^{2}=AD\cdot AC$，$\frac{BD}{BC}=\frac{\sqrt{5}-1}{2}$，则$BD = 2(\sqrt{5}-1)cm$。
综上，（1）已证$\angle ABC=\angle ADB$；（2）$BD=(2\sqrt{5}-2)cm$。

5. (推理能力)[2023·沅江模拟]如图,在$△ABC$中,点D在边AB上,且$BD=$$DC=AC$,已知$∠ACE=108^{\circ },BC=2.$
(1)求$∠B$的度数.$36^{\circ}$
(2)我们把有一个内角等于$36^{\circ }$的等腰三角形称为黄金三角形,它的腰长与底边长的比(或者底边长与腰长的比)等于黄金比$\frac {\sqrt {5}-1}{2}.$
①写出图中所有的黄金三角形,选一个说明理由;$\triangle ABC,\triangle DBC,\triangle CAD$
②求AD的长.$3-\sqrt{5}$

答案： 1. （1）
设$\angle B = x$。
因为$BD = DC$，所以$\angle BCD=\angle B = x$，则$\angle ADC=\angle B+\angle BCD = 2x$。
又因为$DC = AC$，所以$\angle A=\angle ADC = 2x$。
已知$\angle ACE = 108^{\circ}$，$\angle ACE=\angle B+\angle A$，即$x + 2x=108^{\circ}$。
解方程$3x = 108^{\circ}$，得$x = 36^{\circ}$，所以$\angle B = 36^{\circ}$。
2. （2）①
图中的黄金三角形有$\triangle BDC$，$\triangle ABC$，$\triangle ACD$。
选$\triangle BDC$说明理由：
因为$BD = DC$，$\angle B = 36^{\circ}$，所以$\triangle BDC$是等腰三角形，且有一个内角$\angle B = 36^{\circ}$，所以$\triangle BDC$是黄金三角形。
选$\triangle ABC$说明理由：
由（1）知$\angle B = 36^{\circ}$，$\angle A = 2x = 72^{\circ}$，则$\angle ACB=180^{\circ}-\angle A - \angle B=72^{\circ}$，$\angle A=\angle ACB$，$\triangle ABC$是等腰三角形，$\angle B = 36^{\circ}$，所以$\triangle ABC$是黄金三角形。
选$\triangle ACD$说明理由：
因为$DC = AC$，$\angle ADC = 2x = 72^{\circ}$，则$\angle ACD = 180^{\circ}-2×72^{\circ}=36^{\circ}$，$\triangle ACD$是等腰三角形，且有一个内角$\angle ACD = 36^{\circ}$，所以$\triangle ACD$是黄金三角形。
3. （2）②
因为$\triangle ABC$是黄金三角形，$\angle B = 36^{\circ}$，$BC = 2$，$\triangle ABC$中$AC = BC = 2$（$\angle A=\angle ACB = 72^{\circ}$）。
设$AD = y$，则$BD = DC = AC = 2$，$AB=y + 2$。
因为$\triangle ABC$是黄金三角形，根据黄金三角形的性质（腰长与底边长的比等于黄金比$\frac{\sqrt{5}-1}{2}$），这里$AC$为腰，$BC$为底（也可根据相似等方法），由$\triangle BDC\sim\triangle ABC$（$\angle B=\angle B$，$\angle BCD=\angle A$）。
则$\frac{BD}{AB}=\frac{BC}{AC}$，即$\frac{2}{y + 2}=\frac{y}{2}$（由$\triangle BDC$和$\triangle ABC$的边的关系，$BD = DC$，$AC = BC$，利用相似比$\frac{BD}{AB}=\frac{BC}{AC}$，又$DC = AC$，$\triangle BDC$中$BD = DC$，$\triangle ABC$中$AC = BC$，根据相似$\frac{BD}{AB}=\frac{BC}{AC}$，且$DC = AC$，$BD = DC$，可得$\frac{BD}{AB}=\frac{AD}{BD}$）。
得到方程$y^{2}+2y - 4 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a = 1,b = 2,c=-4)$，根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，这里$y=\frac{-2\pm\sqrt{4 + 16}}{2}=\frac{-2\pm2\sqrt{5}}{2}=-1\pm\sqrt{5}$。
因为$y\gt0$，所以$y=\sqrt{5}-1$，即$AD=\sqrt{5}-1$。
综上，（1）$\angle B = 36^{\circ}$；（2）①黄金三角形有$\triangle BDC$，$\triangle ABC$，$\triangle ACD$；②$AD=\sqrt{5}-1$。