《2025年全效学习学业评价方案九年级数学上册北师大版》

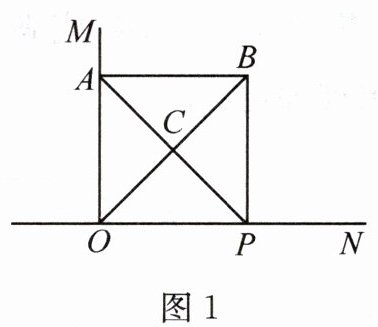
9. [2024·大连期末改编]已知$\angle MON = 90^{\circ}$，点$A$在$OM$上，$OA = 2$，动点$P$在直线$ON$上，连接$AP$并以$AP$为斜边作等腰直角三角形$ABP$，$\angle ABP = 90^{\circ}$，连接$OB$，直线$OB$交直线$AP$于点$C$。当$OP = 2$时（如图1），点$P$开始向左运动。
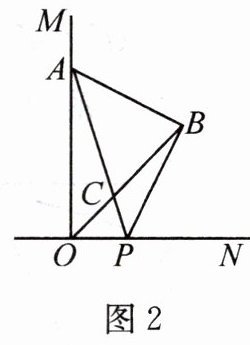
（1）如图2，当点$P$在点$O$的右侧时，
①$\angle BPA =$45$^{\circ}$；
②求证：$\angle BAO=\angle ACB$。


（2）当点$P$在点$O$的左侧运动时，设$OP = x$，$\triangle OBP$的面积为$S$，画出图形，求$S$与$x$的函数表达式。

答案： $(1)$
- ①
因为$\triangle ABP$是等腰直角三角形，$\angle ABP = 90^{\circ}$，根据等腰直角三角形的性质：等腰直角三角形的两个底角相等，且都等于$(180^{\circ}-\angle ABP)÷2$，所以$\angle BPA=(180^{\circ} - 90^{\circ})÷2 = 45^{\circ}$。
- ②
解（证明）：
因为$\angle MON=\angle ABP = 90^{\circ}$，
在$\triangle AOC$中，$\angle AOC+\angle OAC+\angle ACO = 180^{\circ}$；在$\triangle BPC$中，$\angle BPC+\angle PBC+\angle BCP = 180^{\circ}$，
又因为$\angle ACO=\angle BCP$（对顶角相等），$\angle AOC = 90^{\circ}$，$\angle BPC = 45^{\circ}$，$\angle PBC = 45^{\circ}$，
所以$\angle BAO=\angle ACB$。
$(2)$
过点$B$作$BD\perp ON$于点$D$，作$BE\perp OM$于点$E$。
因为$\angle ABP = 90^{\circ}$，$\angle AOB+\angle ABP+\angle BPO+\angle BAP = 360^{\circ}$，$\angle AOB+\angle BAP=\angle BPO+\angle BEO$（四边形内角和为$360^{\circ}$），且$\angle ABE+\angle EBP=\angle DBP+\angle EBP = 90^{\circ}$，所以$\angle ABE=\angle DBP$。
又因为$\angle AEB=\angle PDB = 90^{\circ}$，$AB = BP$，所以$\triangle ABE\cong\triangle PBD(AAS)$。
则$BE = BD$，$AE = PD$。
因为$OA = 2$，$OP=x$，设$OE = BD = h$，$AE = 2 - h$，$PD=h - x$，所以$2 - h=h - x$，解得$h=\frac{x + 2}{2}$。
根据三角形面积公式$S=\frac{1}{2}×底×高$，对于$\triangle OBP$，底为$OP = x$，高为$BD$，所以$S=\frac{1}{2}× OP× BD=\frac{1}{2}× x×\frac{x + 2}{2}=\frac{1}{4}x^{2}+\frac{1}{2}x$（$x\gt0$）。
综上，答案依次为：$(1)$①$\boldsymbol{45}$；②证明过程如上述；$(2)$$\boldsymbol{S=\frac{1}{4}x^{2}+\frac{1}{2}x(x\gt0)}$ 。