第105页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. [2023·江西]《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A,B,Q在同一水平线上,$∠ABC$和$∠AQP$均为直角,AP与BC相交于点D.若测得$AB=40cm$,$BD=20cm$,$AQ=12m$,则树高$PQ=$

6
m.
答案:
6
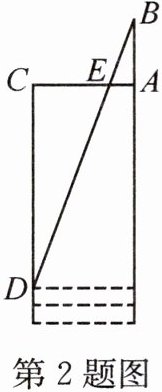
2. [2022·嘉兴]如图,在$\triangle ABC$中,$∠ABC=90^{\circ }$,$∠A=60^{\circ }$,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,则直尺的宽BD为

$\frac{2\sqrt{3}}{3}$
.
答案:
$\frac{2\sqrt{3}}{3}$
1. 如图,为了测量山坡的护坡石坝高,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿上AD长为1m时,它离地面的高度DE为0.6m,则坝高CF为

2.7
m.
答案:
2.7
2. 《九章算术》中记载了一种测量水井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得$AB=1m$,$AC=1.6m$,$AE=0.4m$,那么CD为
3
m.
答案:
3
3. [2023秋·沈阳月考]下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.
|题目|测量小河的宽度(AB的长)|
|----|----|
|测量目标示意图| |
|
|相关数据|$BC=1.5m$,$DE=2m$,$BD=4m$.|
小河的宽度为
|题目|测量小河的宽度(AB的长)|
|----|----|
|测量目标示意图|
 |
||相关数据|$BC=1.5m$,$DE=2m$,$BD=4m$.|
小河的宽度为
12
m.
答案:
解:
因为$BC// DE$,所以$\triangle ABC\sim\triangle ADE$。
根据相似三角形的性质:相似三角形对应边成比例,可得$\frac{AB}{AD}=\frac{BC}{DE}$。
设$AB = x$米,因为$AD=AB + BD$,$BD = 4$米,所以$AD=(x + 4)$米。
已知$BC = 1.5$米,$DE = 2$米,代入$\frac{AB}{AD}=\frac{BC}{DE}$可得:
$\frac{x}{x + 4}=\frac{1.5}{2}$
交叉相乘得:$2x=1.5×(x + 4)$
去括号:$2x=1.5x+6$
移项:$2x-1.5x=6$
合并同类项:$0.5x=6$
解得:$x = 12$。
所以小河的宽度$AB$为$12$米。
因为$BC// DE$,所以$\triangle ABC\sim\triangle ADE$。
根据相似三角形的性质:相似三角形对应边成比例,可得$\frac{AB}{AD}=\frac{BC}{DE}$。
设$AB = x$米,因为$AD=AB + BD$,$BD = 4$米,所以$AD=(x + 4)$米。
已知$BC = 1.5$米,$DE = 2$米,代入$\frac{AB}{AD}=\frac{BC}{DE}$可得:
$\frac{x}{x + 4}=\frac{1.5}{2}$
交叉相乘得:$2x=1.5×(x + 4)$
去括号:$2x=1.5x+6$
移项:$2x-1.5x=6$
合并同类项:$0.5x=6$
解得:$x = 12$。
所以小河的宽度$AB$为$12$米。
4. 某数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长1m的竹竿的影长为0.8m,同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图所示).若墙壁上影长为3m,落在地面上的影长为4m,则树高为

8
m.
答案:
8
查看更多完整答案,请扫码查看


