《2025年全效学习学业评价方案九年级数学上册北师大版》

1. [2023·徐州]下列事件中的必然事件是（A）
A. 地球绕着太阳转
B. 射击运动员射击一次，命中靶心
C. 天空出现三个太阳
D. 经过有交通信号灯的路口，遇到红灯

答案： A

2. 一个不透明的盒子里装有除颜色外其余均相同的2个黑球和2个白球.
(1)摇匀后随机从中摸出1个球，不放回，再随机摸出第2个球，则两次摸球摸到一个白球和一个黑球的概率为$\frac{2}{3}$.请用画树状图或列表的方法进行说明.
(2)盒外有若干个黑球(与盒内黑球完全相同)，往盒子内加入2个黑球，能使摇匀后从中任意摸出一球是黑球的概率是$\frac {2}{3}$.

答案：
(1)$\frac{2}{3}$
(2)2

3. [2023春·沈阳和平区期末]一个口袋中装有4个白球和6个红球，这些球除颜色外完全相同，将口袋中的球搅拌均匀.
(1)随机摸出一球，发现是白球.
①如果将这个白球放回，再摸出一球，那么它是白球的概率是$\frac{2}{5}$；
②如果这个白球不放回，再摸出一球，那么它是白球的概率是$\frac{1}{3}$.
(2)如果向口袋中加入若干个白球，并取出相同数量的红球，然后再从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有40次摸到红球，那么估计加入了2个白球.

答案：
(1)①$\frac{2}{5}$ ②$\frac{1}{3}$
(2)2

4. [2023秋·西华县期末]在一次数学兴趣小组活动中，张红和李燕两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形，并在每个扇形区域内标上数字).游戏规则如下：两人分别转动甲、乙转盘，转盘停止后，若指针所指区域内两数之和小于12，则张红获胜；若指针所指区域内两数之和大于12，则李燕获胜；若指针所指区域内两数之和等于12，则为平局(若指针停在分界线上，重转).
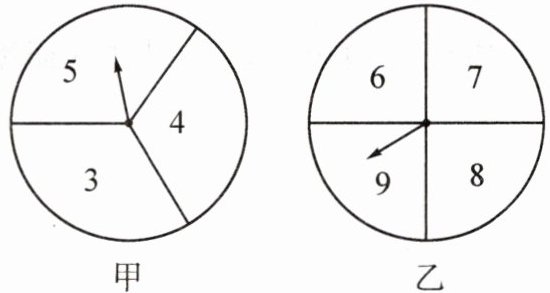
(1)请用列表或画树状图的方法表示上述游戏中两数之和的所有可能结果.
共有 12 种等可能出现的结果，它们是 9，10，11，12，10，11，12，13，11，12，13，14.
(2)判断该游戏对张红和李燕两位同学是否公平？若不公平，请修改上述游戏规则，使该游戏对游戏双方是公平的.
该游戏对张红和李燕两位同学不公平. 为使该游戏对游戏双方是公平的，游戏规则应修改为：两人分别转动甲、乙转盘，转盘停止后，若指针所指区域内两数之和小于 12，则张红获胜；若指针所指区域内两数之和不小于 12，则李燕获胜(若指针停在分界线上，重转).

答案：
(1)共有 12 种等可能出现的结果，它们是 9，10，11，12，10，11，12，13，11，12，13，14.
(2)该游戏对张红和李燕两位同学不公平. 为使该游戏对游戏双方是公平的，游戏规则应修改为：两人分别转动甲、乙转盘，转盘停止后，若指针所指区域内两数之和小于 12，则张红获胜；若指针所指区域内两数之和不小于 12，则李燕获胜(若指针停在分界线上，重转).