《2025年全效学习学业评价方案九年级数学上册北师大版》

1. 用适当的数填空:
(1)$x^{2}-3x+$$\frac {9}{4}$$=(x-$$\frac {3}{2}$$)^{2};$
(2)$x^{2}-3mx+$$\frac {9m^{2}}{4}$$=(x-$$\frac {3m}{2}$$)^{2};$
(3)$a(x^{2}+\frac {b}{a}x+$$\frac {b^{2}}{4a^{2}}$$)=a(x+$$\frac {b}{2a}$$)^{2}.$

答案：
(1)$\frac {9}{4}$ $\frac {3}{2}$
(2)$\frac {9m^{2}}{4}$ $\frac {3m}{2}$
(3)$\frac {b^{2}}{4a^{2}}$ $\frac {b}{2a}$

2. 解下列方程:
(1)$x^{2}-5=\frac {4}{9}$;$x_{1}=\frac {7}{3},x_{2}=-\frac {7}{3}$
(2)$(x-2)^{2}=125$;$x_{1}=2+5\sqrt {5},x_{2}=2-5\sqrt {5}$
(3)$(2x+3)^{2}=(3x+2)^{2}$.$x_{1}=1,x_{2}=-1$

答案：
(1)$x_{1}=\frac {7}{3},x_{2}=-\frac {7}{3}$
(2)$x_{1}=2+5\sqrt {5},x_{2}=2-5\sqrt {5}$
(3)$x_{1}=1,x_{2}=-1$

3. 用配方法解下列一元二次方程:
(1)[2022·无锡]$x^{2}-2x-5=0;$$x_{1}=1+\sqrt {6},x_{2}=1-\sqrt {6}$
(2)$x^{2}-5x+6=0.$$x_{1}=2,x_{2}=3$

答案：
(1)$x_{1}=1+\sqrt {6},x_{2}=1-\sqrt {6}$
(2)$x_{1}=2,x_{2}=3$

4. 某校团体操表演队伍有6行8列,后又增加了51人,使得团体操表演队伍增加的行、列数相同,问增加了多少行多少列?

答案： 增加了3行3列.

5. (模型观念、应用意识)(1)[2023·沈阳皇姑区期中]在皇姑区新开河“口袋公园”的建设过程中,规划将一块长18m、宽10m的矩形场地建设成绿化广场.如图所示,在内部修建三条宽相等的小路,其中一条路与广场的长平行,另两条路与广场的宽平行,其余区域种植绿化,使绿化区域的面积为广场总面积的80%,则该小路的宽为1m.

答案： 1m

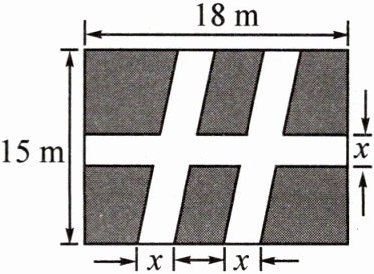
(2)如图,某广场有一块矩形绿地,长18m,宽15m,在绿地中开辟三条道路后,剩余绿地面积为$224m^{2}$,则图中x的值为1.

答案： 1