1. 如图,已知正方形ABCD的边长为1,$\triangle BEF$的周长为2,则$∠EDF$的度数为
$45^{\circ}$
.
答案:
$45^{\circ}$
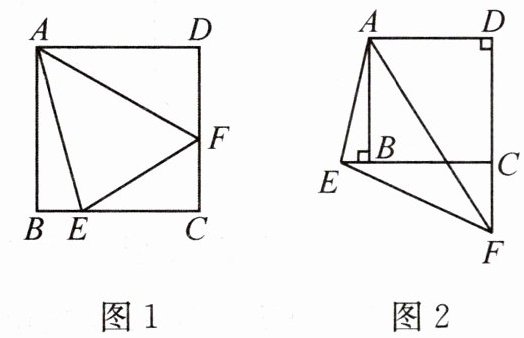
2. 【思维探索】如图,在正方形ABCD中,$AB=4,∠EAF$的两边分别交射线CB,DC于点E,F,$∠EAF=45^{\circ }.$
(1)如图1,当点E,F分别在BC边和CD边上时,$\triangle CEF$的周长为
(2)如图2,当点E,F分别在CB边和DC边的延长线上时,若$CF=2$,求$\triangle CEF$的周长.
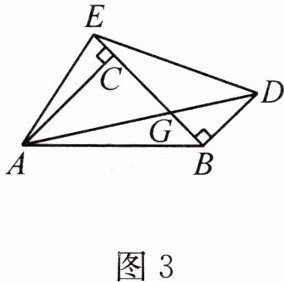
【拓展提升】(3)如图3,在$Rt\triangle ABC$中,$∠ACB=90^{\circ },CA=CB$.过点B作$BD⊥BC$,连接AD.在BC边的延长线上取点E,使$∠EDA=30^{\circ }$,连接AE.当$BD=2,∠EAD=45^{\circ }$时,请直接写出线段CE的长.
(1)如图1,当点E,F分别在BC边和CD边上时,$\triangle CEF$的周长为
8
;(2)如图2,当点E,F分别在CB边和DC边的延长线上时,若$CF=2$,求$\triangle CEF$的周长.
12

【拓展提升】(3)如图3,在$Rt\triangle ABC$中,$∠ACB=90^{\circ },CA=CB$.过点B作$BD⊥BC$,连接AD.在BC边的延长线上取点E,使$∠EDA=30^{\circ }$,连接AE.当$BD=2,∠EAD=45^{\circ }$时,请直接写出线段CE的长.
$EC = \sqrt{3} - 1$

答案:
(1)8
(2)12
(3)$EC = \sqrt{3} - 1$
(1)8
(2)12
(3)$EC = \sqrt{3} - 1$
查看更多完整答案,请扫码查看


