《2025年全效学习学业评价方案九年级数学上册北师大版》

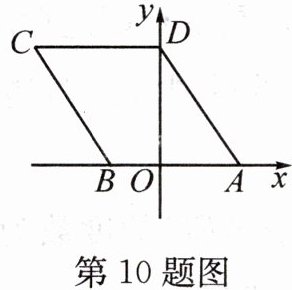
10. 如图,若菱形 ABCD 的顶点 A,B 的坐标分别为$(5,0)$,$(-3,0)$,点 D 在 y 轴上,则点 C 的坐标是$(-8,\sqrt{39})$.

答案： $(-8,\sqrt{39})$

11. (瓜豆原理)如图,在矩形 ABCD 中,$AB=2$,$AD=5$,P 为边 BC 上一点,连接 AP. 以 P 为顶点,PA 为直角边作等腰直角三角形 APQ,连接 CQ,则线段 CQ 的最小值是____$\frac{3\sqrt{2}}{2}$.

答案： $\frac{3\sqrt{2}}{2}$

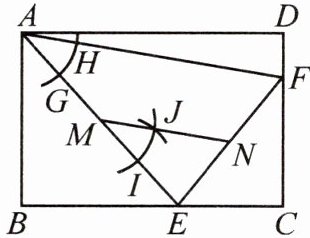
12. [2024·沈阳铁西期中]如图,在矩形 ABCD 中,$AB=8$,$BC=12$,点 F 在边 CD 上,且$CF=6$,点 E 是边 BC 上的一个动点,连接 AE,AF 和 EF,点 M 是线段 AE 的中点. 按照下面的步骤作图:①以点 A 为圆心,以任意长为半径作弧,交 AE 于点 G,交 AF 于点 H;②以点 M 为圆心,以 AG 长为半径作弧,交射线 ME 于点 I;③以点 I 为圆心,以 GH 长为半径作弧,交前弧于点 J,过点 M 作射线 MJ 交线段 EF 于点 N. 则在点 E 从点 B 运动到点 C 的过程中,线段 MN 扫过的图形的周长等于$12+2\sqrt{37}$.

答案： $12+2\sqrt{37}$

13. (10分)[2023秋·浑南区期中]如图,在$□ ABCD$中,E 为线段 CD 的中点,连接 AC,AE,延长 AE,BC 相交于点 F,连接 DF,$∠ACF=90^{\circ }$.
(1)求证:四边形 ACFD 是矩形;略
(2)若$CD=13$,$CF=5$,求四边形 ABCE 的面积.45

答案：

解：

（1）证明：

∵ 四边形 $ABCD$ 是平行四边形，

∴ $AD// BC$。

∴ $\angle ADE=\angle FCE$，$\angle DAE=\angle CFE$。

∵ $E$ 为线段 $CD$ 的中点，

∴ $DE = CE$。

∴ $\triangle ADE\cong\triangle FCE(AAS)$。

∴ $AE = FE$。

∴ 四边形 $ACFD$ 是平行四边形。

∵ $\angle ACF = 90^{\circ}$，

∴ 平行四边形 $ACFD$ 是矩形。

（2）
∵ $CD = 13$，$CF = 5$，

∴ $BC = AD = CF = 5$。

∵ 四边形 $ACFD$ 是矩形，

∴ $\angle CFD = 90^{\circ}$，$AC = DF$。

∴ $DF=\sqrt{CD^{2}-CF^{2}}=\sqrt{13^{2}-5^{2}} = 12$。

∴ $S_{□ ABCD}=BC\cdot AC = 5×12 = 60$。

∵ $\triangle ADE\cong\triangle FCE$，

∴ $S_{\triangle ADE}=S_{\triangle FCE}=\frac{1}{2}S_{\triangle ACF}=\frac{1}{2}×\frac{1}{2}×5×12 = 15$。

∴ $S_{四边形ABCE}=S_{□ ABCD}-S_{\triangle ADE}=60 - 15 = 45$。

14. (10分)[2022·张家界]如图,菱形 ABCD 的对角线 AC,BD 相交于点 O,E 是 CD 的中点,连接 OE,过点 C 作$CF// BD$交 OE 的延长线于点 F,连接 DF.
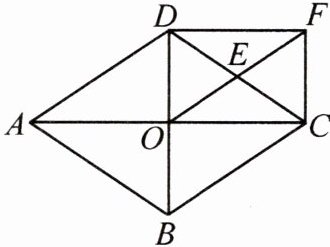
(1)求证:$\triangle ODE\cong \triangle FCE$;略
(2)试判断四边形 ODFC 的形状,并写出证明过程.四边形ODFC是矩形.证明略

答案： 1. （1）证明：
因为$CF// BD$，所以$\angle ODE=\angle FCE$。
因为$E$是$CD$的中点，所以$DE = CE$。
在$\triangle ODE$和$\triangle FCE$中，$\left\{\begin{array}{l}\angle ODE=\angle FCE\\ DE = CE\\ \angle DEO=\angle CEF\end{array}\right.$（对顶角相等）。
根据$ASA$（角 - 边 - 角）判定定理，可得$\triangle ODE\cong\triangle FCE$。
2. （2）解：
四边形$ODFC$是矩形。
证明：
由（1）知$\triangle ODE\cong\triangle FCE$，所以$OE = FE$。
又因为$DE = CE$，所以四边形$ODFC$是平行四边形（对角线互相平分的四边形是平行四边形）。
因为四边形$ABCD$是菱形，所以$AC\perp BD$，即$\angle DOC = 90^{\circ}$。
所以平行四边形$ODFC$是矩形（有一个角是直角的平行四边形是矩形）。
综上，（1）已证$\triangle ODE\cong\triangle FCE$；（2）四边形$ODFC$是矩形。