《2025年全效学习学业评价方案九年级数学上册北师大版》

例3 如图，在矩形ABCD中截取正方形ABMN，使$\frac{BC}{MN}=\frac{MN}{CM}$，已知CM = 3 - $\sqrt{5}$，求AD的长。

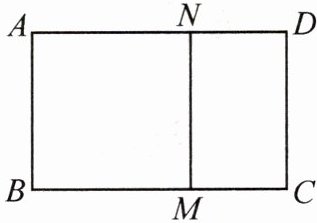
AD的长为2.

答案： 1. 设$MN = x$：
因为四边形$ABMN$是正方形，所以$BC = AD$，$BC=BM + CM$，且$BM = MN=x$，$CM = 3-\sqrt{5}$，那么$BC=x+(3 - \sqrt{5})$。
已知$\frac{BC}{MN}=\frac{MN}{CM}$，即$\frac{x+(3 - \sqrt{5})}{x}=\frac{x}{3 - \sqrt{5}}$。
根据比例的性质“交叉相乘相等”可得：$x^{2}=(x + 3-\sqrt{5})(3 - \sqrt{5})$。
展开右边式子：
$(x + 3-\sqrt{5})(3 - \sqrt{5})=x(3 - \sqrt{5})+(3 - \sqrt{5})^{2}$。
先计算$(3 - \sqrt{5})^{2}$，根据完全平方公式$(a - b)^{2}=a^{2}-2ab + b^{2}$（这里$a = 3$，$b=\sqrt{5}$），$(3 - \sqrt{5})^{2}=9-6\sqrt{5}+5=14 - 6\sqrt{5}$。
所以$x^{2}=x(3 - \sqrt{5})+14 - 6\sqrt{5}$。
移项化为一元二次方程的一般形式：$x^{2}-(3 - \sqrt{5})x-(14 - 6\sqrt{5}) = 0$。
对于一元二次方程$ax^{2}+bx + c = 0$（这里$a = 1$，$b=-(3 - \sqrt{5})$，$c=-(14 - 6\sqrt{5})$），根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，先计算$b^{2}-4ac$：
$b^{2}-4ac=(3 - \sqrt{5})^{2}+4(14 - 6\sqrt{5})$。
展开$(3 - \sqrt{5})^{2}+4(14 - 6\sqrt{5})=9-6\sqrt{5}+5+56-24\sqrt{5}$。
合并同类项得$9 + 5+56-(6\sqrt{5}+24\sqrt{5})=70-30\sqrt{5}$。
另一种方法：
由$\frac{BC}{MN}=\frac{MN}{CM}$，设$\frac{MN}{CM}=\frac{BC}{MN}=k$（$k\gt0$），因为$BC=MN + CM$，则$\frac{MN + CM}{MN}=\frac{MN}{CM}$，令$t=\frac{MN}{CM}$（$t\gt0$），则$1+\frac{1}{t}=t$。
方程两边同乘$t$得$t + 1=t^{2}$，即$t^{2}-t - 1=0$。
根据求根公式$t=\frac{1\pm\sqrt{1+4}}{2}=\frac{1\pm\sqrt{5}}{2}$（因为$t\gt0$，所以$t=\frac{1 + \sqrt{5}}{2}$）。
已知$CM = 3-\sqrt{5}$，又因为$\frac{MN}{CM}=\frac{1+\sqrt{5}}{2}$，所以$MN=\frac{1+\sqrt{5}}{2}×(3 - \sqrt{5})$。
展开$\frac{1+\sqrt{5}}{2}×(3 - \sqrt{5})=\frac{3 - \sqrt{5}+3\sqrt{5}-5}{2}=\frac{2\sqrt{5}-2}{2}=\sqrt{5}-1$。
2. 求$AD$的长：
因为$AD=BC$，$BC=MN + CM$。
把$MN=\sqrt{5}-1$，$CM = 3-\sqrt{5}$代入得$AD=(\sqrt{5}-1)+(3 - \sqrt{5})$。
计算$(\sqrt{5}-1)+(3 - \sqrt{5})=\sqrt{5}-1+3-\sqrt{5}=2$。
所以$AD$的长为$2$。

1. 由等积式ma = nb(a，b，m，n均不为0)，能得到比例式（B）
A. $\frac{a}{b}=\frac{m}{n}$
B. $\frac{a}{b}=\frac{n}{m}$
C. $\frac{m}{a}=\frac{n}{b}$
D. $\frac{m}{b}=\frac{a}{n}$

答案： B

2. 如果3x = 4y(x，y均不为0)，那么$\frac{x}{y}=$$\frac{4}{3}$。

答案： $\frac{4}{3}$

3. 若线段c满足$\frac{a}{c}=\frac{c}{b}$，且线段a = 4 cm，b = 9 cm，则线段c =6cm。

答案： 6

4. 如果某地图上A，B两处的图上距离是4 cm，表示这两地的实际距离是20 km，那么实际距离为500 km的两地在地图上的图上距离是100cm。

答案： 100

1. 下列四组线段中，是成比例线段的是（D）
A. 5 cm，6 cm，7 cm，8 cm
B. 3 cm，6 cm，2 cm，5 cm
C. 2 cm，4 cm，6 cm，8 cm
D. 12 cm，8 cm，15 cm，10 cm

答案： D

2. 已知$\frac{a}{b}=\frac{2}{5}$，则$\frac{a + b}{b}$的值为（C）
A. $\frac{2}{5}$
B. $\frac{3}{5}$
C. $\frac{7}{5}$
D. $\frac{2}{3}$

答案： C

3. 已知$\frac{a}{b}=\frac{3}{2}$，则$\frac{2a - b}{a + 2b}=$$\frac{4}{7}$。

答案： $\frac{4}{7}$

4. 下列各组中的a，b，c，d四条线段是否为成比例线段？若为成比例线段，请写出比例式(式中须含全部的4个字母)。
(1)a = 1 cm，b = 3 cm，c = 6 cm，d = 9 cm；不是成比例线段
(2)a = 5 cm，b = 10 cm，c = 15 cm，d = 20 cm；不是成比例线段
(3)a = 1.9 cm，b = 8.1 cm，c = 5.7 cm，d = 2.7 cm；是成比例线段,比例式为a:c = d:b
(4)a = 126 cm，b = 23 cm，c = 14 cm，d = 207 cm。是成比例线段,比例式为a:c = d:b

答案：
(1)不是成比例线段.
(2)不是成比例线段.
(3)是成比例线段,比例式为$a:c = d:b$.
(4)是成比例线段,比例式为$a:c = d:b$.

5. 已知$\frac{a}{b}=\frac{3}{2}$，求下列算式的值。
(1)$\frac{a + b}{b}$；(2)$\frac{2a + b}{3a - 2b}$。

答案： $(1)$ 求$\frac{a + b}{b}$的值
解：
已知$\frac{a}{b}=\frac{3}{2}$，根据分式加法法则$\frac{a + b}{b}=\frac{a}{b}+\frac{b}{b}$。
因为$\frac{b}{b} = 1$，$\frac{a}{b}=\frac{3}{2}$，所以$\frac{a + b}{b}=\frac{3}{2}+1=\frac{3 + 2}{2}=\frac{5}{2}$。
$(2)$ 求$\frac{2a + b}{3a - 2b}$的值
解：
由$\frac{a}{b}=\frac{3}{2}$，可设$a = 3k$（$k\neq0$），因为$\frac{a}{b}=\frac{3}{2}$，所以$b = 2k$。
将$a = 3k$，$b = 2k$代入$\frac{2a + b}{3a - 2b}$可得：
$\frac{2×3k+2k}{3×3k - 2×2k}=\frac{6k + 2k}{9k - 4k}=\frac{8k}{5k}$（$k\neq0$，分式的分子分母同时约去$k$）$=\frac{8}{5}$。
综上，答案依次为$(1)$$\boldsymbol{\frac{5}{2}}$；$(2)$$\boldsymbol{\frac{8}{5}}$。