第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
1. [2023·临沂]在项目化学习中,“水是生命之源”项目组为了解本地区人均淡水消耗量,需要从四名同学(两名男生,两名女生)中随机抽取两人,组成调查小组进行社会调查,恰好抽到一名男生和一名女生的概率是(
A. $\frac{1}{6}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{2}{3}$
D
)A. $\frac{1}{6}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{2}{3}$
答案:
D
2. [2023·重庆B卷]有四张完全一样正面分别写有汉字“清”“风”“朗”“月”的卡片,将其背面朝上并洗匀,从中随机抽取一张,记下卡片正面上的汉字后放回,洗匀后再从中随机抽取一张,则抽取的两张卡片上的汉字相同的概率是
$\frac{1}{4}$
.
答案:
$\frac{1}{4}$
3. [2023·山西]中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分.若从这四部著作中随机抽取两本(先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是
$\frac{1}{6}$
.
答案:
$\frac{1}{6}$
4. [2023·牡丹江]甲、乙两名同学玩“石头、剪刀、布”的游戏,随机出手一次,甲获胜的概率是
$\frac{1}{3}$
.
答案:
$\frac{1}{3}$
5. 小明的口袋中有5把相似的钥匙,其中只有两把钥匙能打开教室门锁,但他忘了是哪两把钥匙.
(1)小明从口袋中随机摸出一把钥匙就能打开门锁的概率是
(2)小明随机摸出两把钥匙,其中一把能打开,另一把不能打开门锁,请用画树状图的方法求出这个事件的概率.
(1)小明从口袋中随机摸出一把钥匙就能打开门锁的概率是
$\frac{2}{5}$
;(2)小明随机摸出两把钥匙,其中一把能打开,另一把不能打开门锁,请用画树状图的方法求出这个事件的概率.
设能打开门锁的两把钥匙为$A$、$B$,不能打开门锁的三把钥匙为$C$、$D$、$E$。
画树状图:
开始
第一次摸:$A$
第二次摸:$B$、$C$、$D$、$E$
第一次摸:$B$
第二次摸:$A$、$C$、$D$、$E$
第一次摸:$C$
第二次摸:$A$、$B$、$D$、$E$
第一次摸:$D$
第二次摸:$A$、$B$、$C$、$E$
第一次摸:$E$
第二次摸:$A$、$B$、$C$、$D$
从树状图可知,所有可能的结果有$5×4=20$种。
其中一把能打开,另一把不能打开门锁的情况有12种。
所以这个事件的概率$P=\frac{12}{20}=\frac{3}{5}$。
画树状图:
开始
第一次摸:$A$
第二次摸:$B$、$C$、$D$、$E$
第一次摸:$B$
第二次摸:$A$、$C$、$D$、$E$
第一次摸:$C$
第二次摸:$A$、$B$、$D$、$E$
第一次摸:$D$
第二次摸:$A$、$B$、$C$、$E$
第一次摸:$E$
第二次摸:$A$、$B$、$C$、$D$
从树状图可知,所有可能的结果有$5×4=20$种。
其中一把能打开,另一把不能打开门锁的情况有12种。
所以这个事件的概率$P=\frac{12}{20}=\frac{3}{5}$。
答案:
1. (1)
直接根据概率公式$P(A)=\frac{m}{n}$(其中$n$是总情况数,$m$是事件$A$发生的情况数)计算:
已知$n = 5$(钥匙总数),$m = 2$(能开门的钥匙数),所以$P=\frac{2}{5}$。
2. (2)
设能打开门锁的两把钥匙为$A$、$B$,不能打开门锁的三把钥匙为$C$、$D$、$E$。
画树状图:
第一次摸钥匙有$5$种情况,第二次摸钥匙有$4$种情况。
树状图如下:
开始
第一次摸:$A$
第二次摸:$B$
第二次摸:$C$
第二次摸:$D$
第二次摸:$E$
第一次摸:$B$
第二次摸:$A$
第二次摸:$C$
第二次摸:$D$
第二次摸:$E$
第一次摸:$C$
第二次摸:$A$
第二次摸:$B$
第二次摸:$D$
第二次摸:$E$
第一次摸:$D$
第二次摸:$A$
第二次摸:$B$
第二次摸:$C$
第二次摸:$E$
第一次摸:$E$
第二次摸:$A$
第二次摸:$B$
第二次摸:$C$
第二次摸:$D$
从树状图可知,所有可能的结果$n = 5×4=20$(种)(这里因为摸两把钥匙,$(A,B)$和$(B,A)$是不同的摸取顺序,但结果是一样的,不过在树状图中都列出来了)。
其中一把能打开,另一把不能打开门锁的情况$m=(A,C)+(A,D)+(A,E)+(B,C)+(B,D)+(B,E)+(C,A)+(D,A)+(E,A)+(C,B)+(D,B)+(E,B)=12$(种)。
根据概率公式$P=\frac{m}{n}$,这里$n = 20$,$m = 12$,所以$P=\frac{12}{20}=\frac{3}{5}$。
故答案为:(1)$\frac{2}{5}$;(2)$\frac{3}{5}$。
直接根据概率公式$P(A)=\frac{m}{n}$(其中$n$是总情况数,$m$是事件$A$发生的情况数)计算:
已知$n = 5$(钥匙总数),$m = 2$(能开门的钥匙数),所以$P=\frac{2}{5}$。
2. (2)
设能打开门锁的两把钥匙为$A$、$B$,不能打开门锁的三把钥匙为$C$、$D$、$E$。
画树状图:
第一次摸钥匙有$5$种情况,第二次摸钥匙有$4$种情况。
树状图如下:
开始
第一次摸:$A$
第二次摸:$B$
第二次摸:$C$
第二次摸:$D$
第二次摸:$E$
第一次摸:$B$
第二次摸:$A$
第二次摸:$C$
第二次摸:$D$
第二次摸:$E$
第一次摸:$C$
第二次摸:$A$
第二次摸:$B$
第二次摸:$D$
第二次摸:$E$
第一次摸:$D$
第二次摸:$A$
第二次摸:$B$
第二次摸:$C$
第二次摸:$E$
第一次摸:$E$
第二次摸:$A$
第二次摸:$B$
第二次摸:$C$
第二次摸:$D$
从树状图可知,所有可能的结果$n = 5×4=20$(种)(这里因为摸两把钥匙,$(A,B)$和$(B,A)$是不同的摸取顺序,但结果是一样的,不过在树状图中都列出来了)。
其中一把能打开,另一把不能打开门锁的情况$m=(A,C)+(A,D)+(A,E)+(B,C)+(B,D)+(B,E)+(C,A)+(D,A)+(E,A)+(C,B)+(D,B)+(E,B)=12$(种)。
根据概率公式$P=\frac{m}{n}$,这里$n = 20$,$m = 12$,所以$P=\frac{12}{20}=\frac{3}{5}$。
故答案为:(1)$\frac{2}{5}$;(2)$\frac{3}{5}$。
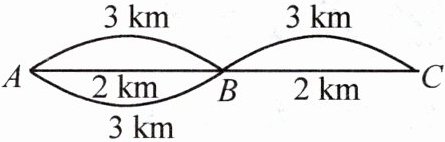
6. [2023秋·淮安期末]如图,从A地到B地共有三条路线,长度分别为3km,2km,3km,从B地到C地共有两条路线,长度分别为3km,2km,小安随机选择路线从A地先到B地再到C地.
(1)小安从A地到B地所走路线长为3km的概率为
(2)用画树状图或列表的方法求小安从A地到C地所走路线总长度为5km的概率.
(1)小安从A地到B地所走路线长为3km的概率为
$\frac{2}{3}$
;(2)用画树状图或列表的方法求小安从A地到C地所走路线总长度为5km的概率.

答案:
1. (1)
从$A$地到$B$地共有$3$条路线,其中长度为$3km$的路线有$2$条。
根据概率公式$P(A)=\frac{m}{n}$(其中$n$是所有可能的结果数,$m$是事件$A$发生的结果数),这里$n = 3$,$m = 2$。
所以小安从$A$地到$B$地所走路线长为$3km$的概率$P=\frac{2}{3}$。
2. (2)
设从$A$到$B$的三条路线为$A_1$($3km$),$A_2$($2km$),$A_3$($3km$);从$B$到$C$的两条路线为$B_1$($3km$),$B_2$($2km$)。
列表如下:
| $A - B$ | $B - C$ | $A - C$总长度($km$) |
| ---- | ---- | ---- |
| $A_1$ | $B_1$ | $3 + 3=6$ |
| $A_1$ | $B_2$ | $3 + 2 = 5$ |
| $A_2$ | $B_1$ | $2+3 = 5$ |
| $A_2$ | $B_2$ | $2 + 2=4$ |
| $A_3$ | $B_1$ | $3 + 3=6$ |
| $A_3$ | $B_2$ | $3 + 2 = 5$ |
从列表中可以看出,从$A$地到$C$地所有可能的路线总长度情况有$6$种,其中路线总长度为$5km$的情况有$3$种。
根据概率公式$P=\frac{m}{n}$,这里$n = 6$,$m = 3$。
所以小安从$A$地到$C$地所走路线总长度为$5km$的概率$P=\frac{3}{6}=\frac{1}{2}$。
综上,答案依次为:(1)$\frac{2}{3}$;(2)$\frac{1}{2}$。
从$A$地到$B$地共有$3$条路线,其中长度为$3km$的路线有$2$条。
根据概率公式$P(A)=\frac{m}{n}$(其中$n$是所有可能的结果数,$m$是事件$A$发生的结果数),这里$n = 3$,$m = 2$。
所以小安从$A$地到$B$地所走路线长为$3km$的概率$P=\frac{2}{3}$。
2. (2)
设从$A$到$B$的三条路线为$A_1$($3km$),$A_2$($2km$),$A_3$($3km$);从$B$到$C$的两条路线为$B_1$($3km$),$B_2$($2km$)。
列表如下:
| $A - B$ | $B - C$ | $A - C$总长度($km$) |
| ---- | ---- | ---- |
| $A_1$ | $B_1$ | $3 + 3=6$ |
| $A_1$ | $B_2$ | $3 + 2 = 5$ |
| $A_2$ | $B_1$ | $2+3 = 5$ |
| $A_2$ | $B_2$ | $2 + 2=4$ |
| $A_3$ | $B_1$ | $3 + 3=6$ |
| $A_3$ | $B_2$ | $3 + 2 = 5$ |
从列表中可以看出,从$A$地到$C$地所有可能的路线总长度情况有$6$种,其中路线总长度为$5km$的情况有$3$种。
根据概率公式$P=\frac{m}{n}$,这里$n = 6$,$m = 3$。
所以小安从$A$地到$C$地所走路线总长度为$5km$的概率$P=\frac{3}{6}=\frac{1}{2}$。
综上,答案依次为:(1)$\frac{2}{3}$;(2)$\frac{1}{2}$。
7. (数据观念)[2022·玉林]问题情境:
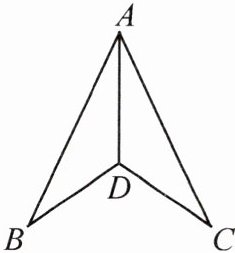
在数学探究活动中,老师给出了如图所示的图形及下面三个等式:
①$AB = AC$;
②$DB = DC$;
③$\angle BAD = \angle CAD$.
若以其中两个等式作为已知条件,能否得到余下一个等式成立?
解决方案:探究$\triangle ABD$与$\triangle ACD$全等.
问题解决:
(1)当选择①②作为已知条件时,$\triangle ABD$与$\triangle ACD$全等吗?
(2)当任意选择两个等式作为已知条件时,请用画树状图法或列表法求$\triangle ABD \cong \triangle ACD$的概率.
解:列表如下:
| | ① | ② | ③ |
|--|--|--|--|
| ① | - | $(①,②)$ | $(①,③)$ |
| ② | $(②,①)$ | - | $(②,③)$ |
| ③ | $(③,①)$ | $(③,②)$ | - |
从表中可以看出,一共有$6$种等可能的情况。
当选择$(①,②)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\DB = DC\\AD = AD\end{array}\right.$,根据$SSS$,$\triangle ABD\cong\triangle ACD$。
当选择$(①,③)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\\angle BAD=\angle CAD\\AD = AD\end{array}\right.$,根据$SAS$(边 - 角 - 边),$\triangle ABD\cong\triangle ACD$。
当选择$(②,③)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}DB = DC\\\angle BAD=\angle CAD\\AD = AD\end{array}\right.$,根据$SAS$,$\triangle ABD\cong\triangle ACD$。
所以$\triangle ABD\cong\triangle ACD$的情况有$3$种。
根据概率公式$P(A)=\frac{m}{n}$(其中$n$是所有等可能的结果数,$m$是事件$A$发生的结果数),则$P(\triangle ABD\cong\triangle ACD)=\frac{3}{6}=\frac{1}{2}$。
在数学探究活动中,老师给出了如图所示的图形及下面三个等式:
①$AB = AC$;
②$DB = DC$;
③$\angle BAD = \angle CAD$.
若以其中两个等式作为已知条件,能否得到余下一个等式成立?
解决方案:探究$\triangle ABD$与$\triangle ACD$全等.
问题解决:
(1)当选择①②作为已知条件时,$\triangle ABD$与$\triangle ACD$全等吗?
全等
(填“全等”或“不全等”),理由是$SSS$(边边边)
.(2)当任意选择两个等式作为已知条件时,请用画树状图法或列表法求$\triangle ABD \cong \triangle ACD$的概率.

解:列表如下:
| | ① | ② | ③ |
|--|--|--|--|
| ① | - | $(①,②)$ | $(①,③)$ |
| ② | $(②,①)$ | - | $(②,③)$ |
| ③ | $(③,①)$ | $(③,②)$ | - |
从表中可以看出,一共有$6$种等可能的情况。
当选择$(①,②)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\DB = DC\\AD = AD\end{array}\right.$,根据$SSS$,$\triangle ABD\cong\triangle ACD$。
当选择$(①,③)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\\angle BAD=\angle CAD\\AD = AD\end{array}\right.$,根据$SAS$(边 - 角 - 边),$\triangle ABD\cong\triangle ACD$。
当选择$(②,③)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}DB = DC\\\angle BAD=\angle CAD\\AD = AD\end{array}\right.$,根据$SAS$,$\triangle ABD\cong\triangle ACD$。
所以$\triangle ABD\cong\triangle ACD$的情况有$3$种。
根据概率公式$P(A)=\frac{m}{n}$(其中$n$是所有等可能的结果数,$m$是事件$A$发生的结果数),则$P(\triangle ABD\cong\triangle ACD)=\frac{3}{6}=\frac{1}{2}$。
答案:
1. (1)
答案:全等,$SSS$(边边边)。
解析:在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\DB = DC\\AD = AD\end{array}\right.$(公共边),根据$SSS$(边 - 边 - 边)判定定理,可得$\triangle ABD\cong\triangle ACD$。
2. (2)
解:列表如下:
| | ① | ② | ③ |
|--|--|--|--|
| ① | - | $(①,②)$ | $(①,③)$ |
| ② | $(②,①)$ | - | $(②,③)$ |
| ③ | $(③,①)$ | $(③,②)$ | - |
从表中可以看出,一共有$6$种等可能的情况。
当选择$(①,②)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\DB = DC\\AD = AD\end{array}\right.$,根据$SSS$,$\triangle ABD\cong\triangle ACD$。
当选择$(①,③)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\\angle BAD=\angle CAD\\AD = AD\end{array}\right.$,根据$SAS$(边 - 角 - 边),$\triangle ABD\cong\triangle ACD$。
当选择$(②,③)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}DB = DC\\\angle BAD=\angle CAD\\AD = AD\end{array}\right.$,根据$SAS$,$\triangle ABD\cong\triangle ACD$。
所以$\triangle ABD\cong\triangle ACD$的情况有$3$种。
根据概率公式$P(A)=\frac{m}{n}$(其中$n$是所有等可能的结果数,$m$是事件$A$发生的结果数),则$P(\triangle ABD\cong\triangle ACD)=\frac{3}{6}=\frac{1}{2}$。
综上,(1)全等,$SSS$;(2)$\frac{1}{2}$。
答案:全等,$SSS$(边边边)。
解析:在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\DB = DC\\AD = AD\end{array}\right.$(公共边),根据$SSS$(边 - 边 - 边)判定定理,可得$\triangle ABD\cong\triangle ACD$。
2. (2)
解:列表如下:
| | ① | ② | ③ |
|--|--|--|--|
| ① | - | $(①,②)$ | $(①,③)$ |
| ② | $(②,①)$ | - | $(②,③)$ |
| ③ | $(③,①)$ | $(③,②)$ | - |
从表中可以看出,一共有$6$种等可能的情况。
当选择$(①,②)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\DB = DC\\AD = AD\end{array}\right.$,根据$SSS$,$\triangle ABD\cong\triangle ACD$。
当选择$(①,③)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}AB = AC\\\angle BAD=\angle CAD\\AD = AD\end{array}\right.$,根据$SAS$(边 - 角 - 边),$\triangle ABD\cong\triangle ACD$。
当选择$(②,③)$时:
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l}DB = DC\\\angle BAD=\angle CAD\\AD = AD\end{array}\right.$,根据$SAS$,$\triangle ABD\cong\triangle ACD$。
所以$\triangle ABD\cong\triangle ACD$的情况有$3$种。
根据概率公式$P(A)=\frac{m}{n}$(其中$n$是所有等可能的结果数,$m$是事件$A$发生的结果数),则$P(\triangle ABD\cong\triangle ACD)=\frac{3}{6}=\frac{1}{2}$。
综上,(1)全等,$SSS$;(2)$\frac{1}{2}$。
查看更多完整答案,请扫码查看


