《2025年全效学习学业评价方案九年级数学上册北师大版》

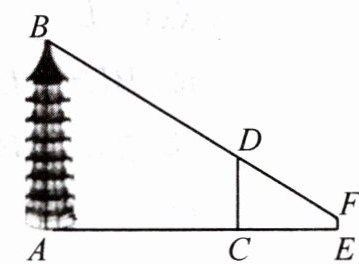
例1 如图，AB表示塔的高度，CD表示竹竿顶端到地面的高度，EF表示人眼到地面的高度，AB，CD，EF在同一平面内，点A，C，E在一条水平直线上.已知$AC=20m$，$CE=10m$，$CD=7m$，$EF=1.4m$，从点F远眺塔顶B，视线恰好经过竹竿的顶端D.根据以上信息，求塔的高度.

塔的高度为18.2m.

答案： 塔的高度为 18.2 m.

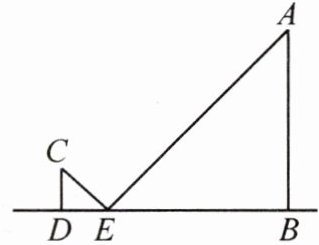
例2 [2023秋·法库县期中]综合实践活动课上，同学们开展了测量本校旗杆高度的实践活动.如图，他们在旗杆底部所在的平地上放置一个平面镜E来测量学校旗杆AB的高度，镜子中心E与旗杆的距离$EB=20m$.当镜子中心E与测量者的距离$DE=2m$时，测量者刚好从镜子中看到旗杆顶部的端点A.已知测量者的身高为1.6m，测量者的眼睛距地面的高度为1.5m.
(1)在计算过程中，C，D之间的距离应是______m；
(2)根据以上测量结果，求出学校旗杆AB的高度.

(1)1.5
(2)学校旗杆 AB 的高度是 15 m.

答案：
(1)1.5
(2)学校旗杆 AB 的高度是 15 m.

例3 如图，为了测量一个大峡谷的宽度，地质勘探人员在对面的岩石上观察到一个特别明显的标志点O，然后在他们所在的这一侧选点A，B，D，使$AB⊥AO$，$DB⊥AB$，然后确定DO和AB的交点C，测得$AC=120m$，$CB=60m$，$BD=50m$.请你帮助他们算出峡谷的宽AO为100m.

答案： 峡谷 AO 的宽是 100 m.