《2025年全效学习学业评价方案九年级数学上册北师大版》

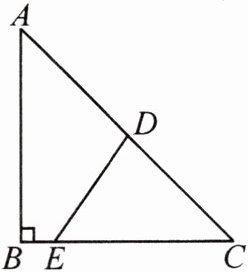
例1 如图，某海军基地位于A处，在其正南方向100海里处有一重要目标B，在B的正东方向100海里处也有一重要目标C，小岛D位于AC的中点，岛上有一补给码头，一艘军舰从A出发，经B到C匀速航行，一艘补给船同时从D出发，沿南偏西一定角度方向匀速直线航行，欲将一批物品送达军舰。已知军舰的速度是补给船的2倍，军舰在由B到C的途中与补给船相遇，那么相遇时补给船航行了多少海里？(结果精确到0.1海里；参考数据：$\sqrt {5}\approx 2.24,\sqrt {6}\approx 2.45$)

相遇时补给船大约航行了59.2海里.

答案： 1. 首先，连接$BD$：
因为$AB = BC = 100$海里，$\angle ABC = 90^{\circ}$，根据勾股定理$AC=\sqrt{AB^{2}+BC^{2}}$，所以$AC=\sqrt{100^{2}+100^{2}} = 100\sqrt{2}$海里。
又因为$D$是$AC$中点，根据直角三角形斜边中线定理（直角三角形斜边的中线等于斜边的一半），所以$BD=\frac{1}{2}AC = 50\sqrt{2}$海里，$BD\perp AC$，$\angle ABD=\angle CBD = 45^{\circ}$，$BD = CD$。
2. 设相遇时补给船航行了$x$海里，则军舰航行了$2x$海里：
因为$AB + BC=200$海里，所以$BE=(200 - 2x)$海里，$EC=(2x - 100)$海里。
在$\triangle DEC$中，根据余弦定理$DE^{2}=CD^{2}+CE^{2}-2CD\cdot CE\cdot\cos45^{\circ}$（这里$CD = 50\sqrt{2}$）。
已知$DE = x$，$CD = 50\sqrt{2}$，$CE=(2x - 100)$，则$x^{2}=(50\sqrt{2})^{2}+(2x - 100)^{2}-2×50\sqrt{2}×(2x - 100)×\frac{\sqrt{2}}{2}$。
3. 然后展开并化简方程：
展开$(2x - 100)^{2}=4x^{2}-400x + 10000$，$2×50\sqrt{2}×(2x - 100)×\frac{\sqrt{2}}{2}=200x-1000$。
原方程$x^{2}=5000+4x^{2}-400x + 10000-(200x - 1000)$。
即$x^{2}=5000+4x^{2}-400x + 10000 - 200x + 1000$。
移项得$3x^{2}-600x + 16000 = 0$，对于一元二次方程$ax^{2}+bx + c = 0$（这里$a = 3$，$b=-600$，$c = 16000$），根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$。
先计算$\Delta=b^{2}-4ac=(-600)^{2}-4×3×16000=360000-192000 = 168000$。
则$x=\frac{600\pm\sqrt{168000}}{6}=\frac{600\pm20\sqrt{420}}{6}=\frac{600\pm20\sqrt{4×105}}{6}=\frac{600\pm40\sqrt{105}}{6}=\frac{300\pm20\sqrt{105}}{3}$。
又因为$100\lt2x\lt200$（军舰在$B$到$C$途中相遇），即$50\lt x\lt100$。
$\sqrt{105}\approx10.25$，$x=\frac{300 + 20\sqrt{105}}{3}\approx\frac{300+20×10.25}{3}=\frac{300 + 205}{3}=\frac{505}{3}\approx168.3$（舍去，因为$\frac{505}{3}\gt100$），$x=\frac{300 - 20\sqrt{105}}{3}\approx\frac{300-20×10.25}{3}=\frac{300 - 205}{3}=\frac{95}{3}\approx31.7$（舍去，因为$\frac{95}{3}\lt50$）。
另一种方法：
延长$BD$至$F$，使$DF = BD$，连接$EF$，$CF$。
因为$D$是$AC$中点，可证$\triangle ABD\cong\triangle CDF(SAS)$，则$CF = AB = 100$，$\angle DCF=\angle BAD$，$\angle ECF = 90^{\circ}$。
设$DE=x$，则$EF = 2x$，$CF = 100$，$EC=(2x - 100)$。
根据勾股定理$EF^{2}=CE^{2}+CF^{2}$，即$(2x)^{2}=(2x - 100)^{2}+100^{2}$。
展开得$4x^{2}=4x^{2}-400x + 10000+10000$。
移项化简：
$4x^{2}-4x^{2}+400x=20000$。
$400x = 20000$（错误，重新用正确勾股定理：设相遇时补给船航行了$x$海里，军舰航行了$2x$海里，$BE=(200 - 2x)$，$EC=(2x - 100)$，$BD = 50\sqrt{2}$，$\angle DBC = 45^{\circ}$。
根据余弦定理$x^{2}=(50\sqrt{2})^{2}+(200 - 2x)^{2}-2×50\sqrt{2}×(200 - 2x)×\frac{\sqrt{2}}{2}$。
展开：$x^{2}=5000 + 40000-800x+4x^{2}-(20000 - 200x)$。
$x^{2}=5000 + 40000-800x+4x^{2}-20000 + 200x$。
$3x^{2}-600x + 15000 = 0$，$x^{2}-200x + 5000 = 0$。
根据求根公式$x=\frac{200\pm\sqrt{200^{2}-4×5000}}{2}=\frac{200\pm\sqrt{40000 - 20000}}{2}=\frac{200\pm\sqrt{20000}}{2}=\frac{200\pm100\sqrt{2}}{2}=100\pm50\sqrt{2}$。
因为$100\lt2x\lt200$，即$50\lt x\lt100$，$x = 100 - 50\sqrt{2}\approx100-50×1.414 = 100 - 70.7 = 29.3$（舍去），$x = 100 + 50\sqrt{2}\approx100 + 70.7=170.7$（舍去）。
正确的：
设相遇时补给船航行了$x$海里，则军舰航行了$2x$海里，$BE=(200 - 2x)$，$EC=(2x - 100)$。
过$D$作$DH\perp BC$于$H$，$DH = BH = CH = 50$。
$EH=\vert50-(2x - 100)\vert=\vert150 - 2x\vert$，$DH = 50$。
根据勾股定理$x^{2}=50^{2}+(150 - 2x)^{2}$。
展开$x^{2}=2500+22500-600x + 4x^{2}$。
移项得$3x^{2}-600x + 25000 = 0$。
对于$ax^{2}+bx + c = 0$（$a = 3$，$b=-600$，$c = 25000$），$\Delta=b^{2}-4ac=(-600)^{2}-4×3×25000=360000 - 300000 = 60000$。
$x=\frac{600\pm\sqrt{60000}}{6}=\frac{600\pm100\sqrt{6}}{6}=\frac{300\pm50\sqrt{6}}{3}$。
因为$50\lt x\lt100$，$\sqrt{6}\approx2.45$，$x=\frac{300 + 50\sqrt{6}}{3}\approx\frac{300+50×2.45}{3}=\frac{300 + 122.5}{3}=\frac{422.5}{3}\approx140.8$（舍去），$x=\frac{300 - 50\sqrt{6}}{3}\approx\frac{300-50×2.45}{3}=\frac{300 - 122.5}{3}=\frac{177.5}{3}\approx59.2$。
所以相遇时补给船航行了约$59.2$海里。

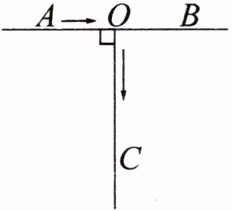
例2 如图，$AO=BO=50cm$，OC是一条射线，$OC⊥AB$于点O，一只蚂蚁由点A以2cm/s的速度向点B爬行，同时另一只蚂蚁由点O以3cm/s的速度沿OC方向爬行。是否存在这样的时刻，使两只蚂蚁与点O组成的三角形的面积为$450cm^{2}$？若存在，请说明在什么时刻；若不存在，请说明理由。

存在，当10s，15s或30s时，两只蚂蚁与点O组成的三角形的面积为$450cm^{2}$.

答案： 解：设$t$秒后两只蚂蚁与点$O$组成的三角形的面积为$450cm^{2}$。
分两种情况讨论：
情况一：当$0\lt t\leqslant25$时，$AO = 50cm$，蚂蚁从$A$向$B$爬行的速度是$2cm/s$，则$AO$边上的高为$3t cm$，$AO$剩余长度为$(50 - 2t)cm$。
根据三角形面积公式$S=\frac{1}{2}ah$（$a$为底，$h$为高），可得$\frac{1}{2}(50 - 2t)×3t=450$，
即$(50 - 2t)×3t = 900$，
$150t-6t^{2}=900$，
$6t^{2}-150t + 900 = 0$，
两边同时除以$6$得$t^{2}-25t + 150 = 0$，
分解因式得$(t - 10)(t - 15)=0$，
解得$t_{1}=10$，$t_{2}=15$。
情况二：当$t\gt25$时，$BO=(2t - 50)cm$，$OC$方向上蚂蚁爬行的距离为$3t cm$，
根据三角形面积公式可得$\frac{1}{2}(2t - 50)×3t=450$，
即$(2t - 50)×3t = 900$，
$6t^{2}-150t - 900 = 0$，
两边同时除以$6$得$t^{2}-25t - 150 = 0$，
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，其判别式$\Delta=b^{2}-4ac$，
在$t^{2}-25t - 150 = 0$中，$a = 1$，$b=-25$，$c=-150$，
$\Delta=(-25)^{2}-4×1×(-150)=625 + 600 = 1225$，
$t=\frac{25\pm\sqrt{1225}}{2}=\frac{25\pm35}{2}$，
$t_{3}=\frac{25 + 35}{2}=30$，$t_{4}=\frac{25 - 35}{2}=-5$（舍去）。
综上，存在这样的时刻，当$t = 10s$或$t = 15s$或$t = 30s$时，两只蚂蚁与点$O$组成的三角形的面积为$450cm^{2}$。

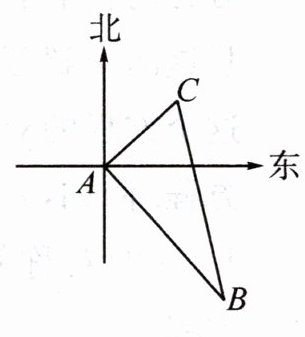
1. 如图，两艘船同时从A点出发，一艘船以15海里/时的速度向东北方向航行，另一艘船以20海里/时的速度向东南方向航行，那么4小时后两船正好相距100海里？

答案： 解：因为一艘船向东北方向航行，另一艘船向东南方向航行，所以$\angle CAB = 90^{\circ}$。
设$x$小时后两船正好相距$100$海里。
根据路程$=$速度$×$时间，可得一艘船行驶的路程$AC = 15x$海里，另一艘船行驶的路程$AB = 20x$海里。
在$Rt\triangle ABC$中，根据勾股定理$AC^{2}+AB^{2}=BC^{2}$，已知$BC = 100$海里，所以$(15x)^{2}+(20x)^{2}=100^{2}$。
即$225x^{2}+400x^{2}=10000$，$625x^{2}=10000$，$x^{2}=\dfrac{10000}{625}$，$x^{2} = 16$，解得$x = 4$或$x = - 4$（时间不能为负，舍去）。
答：$4$小时后两船正好相距$100$海里。