第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
6. 如图,在四边形$ABCD$中,$P$是对角线$BD$的中点,$E$、$F$分别是$AB$、$CD$的中点,$AD = BC$,$\angle FPE = 100^{\circ}$,则$\angle PFE$的度数为____。


答案:
6. 40°
7. 如图,$\triangle ABC$的中线$BE$、$CF$相交于点$G$,连结$EF$。求证:$BG = 2GE$,$CG = 2GF$。
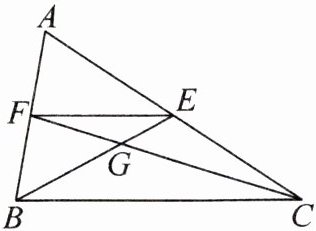

答案:
证明:
因为$BE$、$CF$是$\triangle ABC$的中线,
所以$EF$是$\triangle ABC$的中位线(三角形中线连接顶点与对边中点,$E,F$为两边的中点)。
所以$EF// BC$,且$EF=\frac{1}{2}BC$(三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半)。
在$\triangle BEF$中,因为$EF// BC$,
所以$\triangle EFG\sim\triangle BCG$(平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似)。
所以$\frac{EG}{BG}=\frac{FG}{CG}=\frac{EF}{BC}$。
又因为$EF = \frac{1}{2}BC$,
所以$\frac{EG}{BG}=\frac{FG}{CG}=\frac{1}{2}$。
即$BG = 2GE$,$CG = 2GF$。
因为$BE$、$CF$是$\triangle ABC$的中线,
所以$EF$是$\triangle ABC$的中位线(三角形中线连接顶点与对边中点,$E,F$为两边的中点)。
所以$EF// BC$,且$EF=\frac{1}{2}BC$(三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半)。
在$\triangle BEF$中,因为$EF// BC$,
所以$\triangle EFG\sim\triangle BCG$(平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似)。
所以$\frac{EG}{BG}=\frac{FG}{CG}=\frac{EF}{BC}$。
又因为$EF = \frac{1}{2}BC$,
所以$\frac{EG}{BG}=\frac{FG}{CG}=\frac{1}{2}$。
即$BG = 2GE$,$CG = 2GF$。
8. 如图,$BM$、$CN$分别平分$\triangle ABC$的外角$\angle ABD$、$\angle ACE$,过点$A$分别作$BM$、$CN$的垂线,垂足分别为$M$、$N$,交$CB$、$BC$的延长线于$D$、$E$,连结$MN$。求证:$MN = \frac{1}{2}(AB + BC + AC)$。
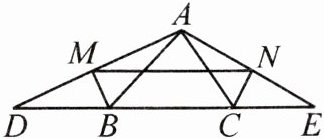

答案:
证明:
1. 证△ABM≌△DBM:
∵BM平分∠ABD,
∴∠ABM=∠DBM。
∵AM⊥BM,
∴∠AMB=∠DMB=90°。
在△ABM和△DBM中,
$\begin{cases} ∠ABM=∠DBM \\ BM=BM \\ ∠AMB=∠DMB \end{cases}$,
∴△ABM≌△DBM(ASA)。
∴AM=DM,DB=AB。即M为AD中点,DB=AB。
2. 证△ACN≌△ECN:
∵CN平分∠ACE,
∴∠ACN=∠ECN。
∵AN⊥CN,
∴∠ANC=∠ENC=90°。
在△ACN和△ECN中,
$\begin{cases} ∠ACN=∠ECN \\ CN=CN \\ ∠ANC=∠ENC \end{cases}$,
∴△ACN≌△ECN(ASA)。
∴AN=EN,EC=AC。即N为AE中点,EC=AC。
3. 证MN为△ADE中位线:
∵M为AD中点,N为AE中点,
∴MN是△ADE的中位线。
∴MN=$\frac{1}{2}$DE(三角形中位线定理)。
4. 计算DE:
∵D、B、C、E共线,
∴DE=DB+BC+CE。
又
∵DB=AB,EC=AC,
∴DE=AB+BC+AC。
5. 结论:
∴MN=$\frac{1}{2}$DE=$\frac{1}{2}$(AB+BC+AC)。
即证得$MN = \frac{1}{2}(AB + BC + AC)$。
1. 证△ABM≌△DBM:
∵BM平分∠ABD,
∴∠ABM=∠DBM。
∵AM⊥BM,
∴∠AMB=∠DMB=90°。
在△ABM和△DBM中,
$\begin{cases} ∠ABM=∠DBM \\ BM=BM \\ ∠AMB=∠DMB \end{cases}$,
∴△ABM≌△DBM(ASA)。
∴AM=DM,DB=AB。即M为AD中点,DB=AB。
2. 证△ACN≌△ECN:
∵CN平分∠ACE,
∴∠ACN=∠ECN。
∵AN⊥CN,
∴∠ANC=∠ENC=90°。
在△ACN和△ECN中,
$\begin{cases} ∠ACN=∠ECN \\ CN=CN \\ ∠ANC=∠ENC \end{cases}$,
∴△ACN≌△ECN(ASA)。
∴AN=EN,EC=AC。即N为AE中点,EC=AC。
3. 证MN为△ADE中位线:
∵M为AD中点,N为AE中点,
∴MN是△ADE的中位线。
∴MN=$\frac{1}{2}$DE(三角形中位线定理)。
4. 计算DE:
∵D、B、C、E共线,
∴DE=DB+BC+CE。
又
∵DB=AB,EC=AC,
∴DE=AB+BC+AC。
5. 结论:
∴MN=$\frac{1}{2}$DE=$\frac{1}{2}$(AB+BC+AC)。
即证得$MN = \frac{1}{2}(AB + BC + AC)$。
9. [2024·凉州区二模]如图,在四边形$ABCD$中,$AC = BD$,$AC$、$BD$交于点$O$,$E$、$F$分别是$AB$、$CD$中点,$EF$分别交$AC$、$BD$于点$H$、$G$。求证:$OG = OH$。
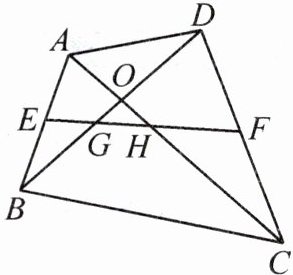

答案:
证明:取AD的中点M,连接EM、FM。
∵E是AB中点,M是AD中点,
∴EM是△ABD的中位线,
∴EM//BD,且EM=1/2 BD。
∵F是CD中点,M是AD中点,
∴FM是△ACD的中位线,
∴FM//AC,且FM=1/2 AC。
∵AC=BD,
∴EM=FM,
∴△EMF中,∠MEF=∠MFE。
∵EM//BD,
∴∠MEF=∠OGH(两直线平行,内错角相等)。
∵FM//AC,
∴∠MFE=∠OHG(两直线平行,内错角相等)。
∴∠OGH=∠OHG,
∴OG=OH(等角对等边)。
∵E是AB中点,M是AD中点,
∴EM是△ABD的中位线,
∴EM//BD,且EM=1/2 BD。
∵F是CD中点,M是AD中点,
∴FM是△ACD的中位线,
∴FM//AC,且FM=1/2 AC。
∵AC=BD,
∴EM=FM,
∴△EMF中,∠MEF=∠MFE。
∵EM//BD,
∴∠MEF=∠OGH(两直线平行,内错角相等)。
∵FM//AC,
∴∠MFE=∠OHG(两直线平行,内错角相等)。
∴∠OGH=∠OHG,
∴OG=OH(等角对等边)。
10. (模型观念)[2023·山西]阅读与思考。
下面是一位同学的数学学习笔记,请仔细阅读并完成相应任务。
瓦里尼翁平行四边形。
我们知道,如图1,在四边形$ABCD$中,点$E$、$F$、$G$、$H$分别是边$AB$、$BC$、$CD$、$DA$的中点,顺次连结$E$、$F$、$G$、$H$,得到的四边形$EFGH$是平行四边形。
我查阅了许多资料,得知这个平行四边形$EFGH$被称为瓦里尼翁平行四边形。瓦里尼翁(Varingnon,Pierre 1654—1722)是法国数学家、力学家。瓦里尼翁平行四边形与原四边形关系密切。
①当原四边形的对角线满足一定关系时,瓦里尼翁平行四边形可能是菱形、矩形或正方形。
②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系。
③瓦里尼翁平行四边形的面积等于原四边形面积的一半。此结论证明如下:
证明:如图2,连结$AC$,分别交$EH$、$FG$于点$P$、$Q$,过点$D$作$DM \perp AC$于点$M$,交$HG$于点$N$。
$\because H$、$G$分别为$AD$、$CD$的中点,
$\therefore HG // AC$,$HG = \frac{1}{2}AC$,(依据1)
$\therefore \frac{DN}{NM} = \frac{DG}{GC}$。
$\because DG = GC$,$\therefore DN = NM = \frac{1}{2}DM$。
$\because$四边形$EFGH$是瓦里尼翁平行四边形,
$\therefore HE // GF$,即$HP // GQ$。
$\because HG // AC$,即$HG // PQ$,
$\therefore$四边形$HPQG$是平行四边形,(依据2)
$\therefore S_{□ HPQG} = HG \cdot MN = \frac{1}{2}HG \cdot DM$。
$\because S_{\triangle ADC} = \frac{1}{2}AC \cdot DM = HG \cdot DM$,
$\therefore S_{□ HPQG} = \frac{1}{2}S_{\triangle ADC}$。同理,……
任务:
(1)材料中的依据1是指:____;
依据2是指:____。
(2)请用刻度尺、三角板等工具,画一个四边形$ABCD$及它的瓦里尼翁平行四边形$EFGH$,使得四边形$EFGH$为矩形。(要求同时画出四边形$ABCD$的对角线)
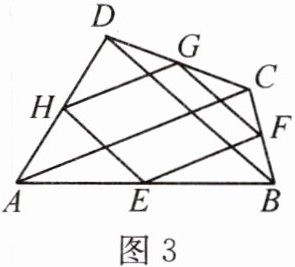
(3)在图1中,分别连结$AC$、$BD$得到图3,请猜想瓦里尼翁平行四边形$EFGH$的周长与对角线$AC$、$BD$长度的关系,并证明你的结论。

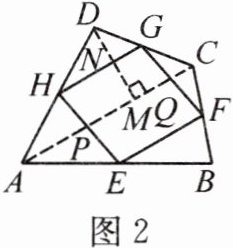
下面是一位同学的数学学习笔记,请仔细阅读并完成相应任务。
瓦里尼翁平行四边形。
我们知道,如图1,在四边形$ABCD$中,点$E$、$F$、$G$、$H$分别是边$AB$、$BC$、$CD$、$DA$的中点,顺次连结$E$、$F$、$G$、$H$,得到的四边形$EFGH$是平行四边形。
我查阅了许多资料,得知这个平行四边形$EFGH$被称为瓦里尼翁平行四边形。瓦里尼翁(Varingnon,Pierre 1654—1722)是法国数学家、力学家。瓦里尼翁平行四边形与原四边形关系密切。
①当原四边形的对角线满足一定关系时,瓦里尼翁平行四边形可能是菱形、矩形或正方形。
②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系。
③瓦里尼翁平行四边形的面积等于原四边形面积的一半。此结论证明如下:
证明:如图2,连结$AC$,分别交$EH$、$FG$于点$P$、$Q$,过点$D$作$DM \perp AC$于点$M$,交$HG$于点$N$。
$\because H$、$G$分别为$AD$、$CD$的中点,
$\therefore HG // AC$,$HG = \frac{1}{2}AC$,(依据1)
$\therefore \frac{DN}{NM} = \frac{DG}{GC}$。
$\because DG = GC$,$\therefore DN = NM = \frac{1}{2}DM$。
$\because$四边形$EFGH$是瓦里尼翁平行四边形,
$\therefore HE // GF$,即$HP // GQ$。
$\because HG // AC$,即$HG // PQ$,
$\therefore$四边形$HPQG$是平行四边形,(依据2)
$\therefore S_{□ HPQG} = HG \cdot MN = \frac{1}{2}HG \cdot DM$。
$\because S_{\triangle ADC} = \frac{1}{2}AC \cdot DM = HG \cdot DM$,
$\therefore S_{□ HPQG} = \frac{1}{2}S_{\triangle ADC}$。同理,……
任务:
(1)材料中的依据1是指:____;
依据2是指:____。
(2)请用刻度尺、三角板等工具,画一个四边形$ABCD$及它的瓦里尼翁平行四边形$EFGH$,使得四边形$EFGH$为矩形。(要求同时画出四边形$ABCD$的对角线)
(3)在图1中,分别连结$AC$、$BD$得到图3,请猜想瓦里尼翁平行四边形$EFGH$的周长与对角线$AC$、$BD$长度的关系,并证明你的结论。



答案:
$(1)$ 分析依据
- 依据$1$:因为$H$、$G$分别为$AD$、$CD$的中点,得出$HG// AC$,$HG = \frac{1}{2}AC$,这是三角形中位线定理(三角形的中位线平行于三角形的第三边,并且等于第三边的一半)。
- 依据$2$:因为$HP// GQ$,$HG// PQ$,得出四边形$HPQG$是平行四边形,这是平行四边形的定义(两组对边分别平行的四边形是平行四边形)。
$(2)$ 画图步骤
- 画一个四边形$ABCD$,使对角线$AC\perp BD$(例如先画两条互相垂直的线段$AC$和$BD$,然后连接$A$、$B$、$C$、$D$构成四边形)。
分别取$AB$、$BC$、$CD$、$DA$的中点$E$、$F$、$G$、$H$,顺次连结$E$、$F$、$G$、$H$,得到的四边形$EFGH$就是矩形(因为原四边形对角线垂直,根据中位线性质可推出瓦里尼翁平行四边形$EFGH$的邻边垂直) 。
$(3)$ 猜想与证明
- 猜想:瓦里尼翁平行四边形$EFGH$的周长等于$AC + BD$。
- 证明:
解:因为$E$、$F$、$G$、$H$分别是边$AB$、$BC$、$CD$、$DA$的中点。
根据三角形中位线定理,在$\triangle ABC$中,$EF// AC$,$EF=\frac{1}{2}AC$;在$\triangle ADC$中,$HG// AC$,$HG = \frac{1}{2}AC$;在$\triangle ABD$中,$EH// BD$,$EH=\frac{1}{2}BD$;在$\triangle BCD$中,$FG// BD$,$FG=\frac{1}{2}BD$。
所以四边形$EFGH$的周长$C = EF + FG+GH + HE$。
将$EF=\frac{1}{2}AC$,$FG=\frac{1}{2}BD$,$GH=\frac{1}{2}AC$,$HE=\frac{1}{2}BD$代入周长公式得:
$C=\frac{1}{2}AC+\frac{1}{2}BD+\frac{1}{2}AC+\frac{1}{2}BD=AC + BD$。
综上,答案依次为:$(1)$三角形中位线定理;平行四边形的定义;$(3)$瓦里尼翁平行四边形$EFGH$的周长等于$AC + BD$。
- 依据$1$:因为$H$、$G$分别为$AD$、$CD$的中点,得出$HG// AC$,$HG = \frac{1}{2}AC$,这是三角形中位线定理(三角形的中位线平行于三角形的第三边,并且等于第三边的一半)。
- 依据$2$:因为$HP// GQ$,$HG// PQ$,得出四边形$HPQG$是平行四边形,这是平行四边形的定义(两组对边分别平行的四边形是平行四边形)。
$(2)$ 画图步骤
- 画一个四边形$ABCD$,使对角线$AC\perp BD$(例如先画两条互相垂直的线段$AC$和$BD$,然后连接$A$、$B$、$C$、$D$构成四边形)。
分别取$AB$、$BC$、$CD$、$DA$的中点$E$、$F$、$G$、$H$,顺次连结$E$、$F$、$G$、$H$,得到的四边形$EFGH$就是矩形(因为原四边形对角线垂直,根据中位线性质可推出瓦里尼翁平行四边形$EFGH$的邻边垂直) 。
$(3)$ 猜想与证明
- 猜想:瓦里尼翁平行四边形$EFGH$的周长等于$AC + BD$。
- 证明:
解:因为$E$、$F$、$G$、$H$分别是边$AB$、$BC$、$CD$、$DA$的中点。
根据三角形中位线定理,在$\triangle ABC$中,$EF// AC$,$EF=\frac{1}{2}AC$;在$\triangle ADC$中,$HG// AC$,$HG = \frac{1}{2}AC$;在$\triangle ABD$中,$EH// BD$,$EH=\frac{1}{2}BD$;在$\triangle BCD$中,$FG// BD$,$FG=\frac{1}{2}BD$。
所以四边形$EFGH$的周长$C = EF + FG+GH + HE$。
将$EF=\frac{1}{2}AC$,$FG=\frac{1}{2}BD$,$GH=\frac{1}{2}AC$,$HE=\frac{1}{2}BD$代入周长公式得:
$C=\frac{1}{2}AC+\frac{1}{2}BD+\frac{1}{2}AC+\frac{1}{2}BD=AC + BD$。
综上,答案依次为:$(1)$三角形中位线定理;平行四边形的定义;$(3)$瓦里尼翁平行四边形$EFGH$的周长等于$AC + BD$。
查看更多完整答案,请扫码查看


