第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
1. 同类二次根式
定 义:几个二次根式化为最简二次根式后,如果被开方数相同,那么这几个二次根式叫做同类二次根式。
2. 二次根式的加减法
法 则:将同类二次根式合并,只需把根号外的式子相加减。不是同类二次根式的不能合并。
步 骤:
(1)化成最简二次根式;
(2)找出同类二次根式;
(3)合并同类二次根式。
3. 二次根式的混合运算
法 则:先算乘方、开方,再算乘除,最后算加减,有括号的先算括号里面的。
定 义:几个二次根式化为最简二次根式后,如果被开方数相同,那么这几个二次根式叫做同类二次根式。
2. 二次根式的加减法
法 则:将同类二次根式合并,只需把根号外的式子相加减。不是同类二次根式的不能合并。
步 骤:
(1)化成最简二次根式;
(2)找出同类二次根式;
(3)合并同类二次根式。
3. 二次根式的混合运算
法 则:先算乘方、开方,再算乘除,最后算加减,有括号的先算括号里面的。
答案:
1.最简二次根式 被开方数相同
例1 下列二次根式中,与$\sqrt{3}$是同类二次根式的是( )
A.$\sqrt{\dfrac{8}{9}}$
B.$\sqrt{27}$
C.$\sqrt{\dfrac{2}{3}}$
D.$\sqrt{18}$
A.$\sqrt{\dfrac{8}{9}}$
B.$\sqrt{27}$
C.$\sqrt{\dfrac{2}{3}}$
D.$\sqrt{18}$
答案:
【例1】B
例2 计算:
(1)$2\sqrt{12}+\sqrt{27}$;
(2)$\sqrt{18}-\sqrt{\dfrac{9}{2}}$;
(3)$\dfrac{2}{3}\sqrt{9x}+6\sqrt{\dfrac{x}{4}}$;
(4)$a^{2}\sqrt{8a}+3a\sqrt{50a^{3}}$。
(1)$2\sqrt{12}+\sqrt{27}$;
(2)$\sqrt{18}-\sqrt{\dfrac{9}{2}}$;
(3)$\dfrac{2}{3}\sqrt{9x}+6\sqrt{\dfrac{x}{4}}$;
(4)$a^{2}\sqrt{8a}+3a\sqrt{50a^{3}}$。
答案:
【例2】
(1)$7\sqrt{3}$
(2)$\frac{3\sqrt{2}}{2}$
(3)$5\sqrt{x}$
(4)$17a^{2}\sqrt{2a}$
(1)$7\sqrt{3}$
(2)$\frac{3\sqrt{2}}{2}$
(3)$5\sqrt{x}$
(4)$17a^{2}\sqrt{2a}$
例3 计算:
(1)$\left(\sqrt{\dfrac{8}{27}}-5\sqrt{3}\right)×\sqrt{6}$;
(2)$(2\sqrt{3}+3\sqrt{2})(2\sqrt{3}-3\sqrt{2})$;
(3)$(4 + 3\sqrt{5})^{2}$;
(4)$(5+\sqrt{6})(5\sqrt{2}-2\sqrt{3})$。
(1)$\left(\sqrt{\dfrac{8}{27}}-5\sqrt{3}\right)×\sqrt{6}$;
(2)$(2\sqrt{3}+3\sqrt{2})(2\sqrt{3}-3\sqrt{2})$;
(3)$(4 + 3\sqrt{5})^{2}$;
(4)$(5+\sqrt{6})(5\sqrt{2}-2\sqrt{3})$。
答案:
【例3】
(1)$\frac{4}{3}-15\sqrt{2}$
(2)$-6$
(3)$61 + 24\sqrt{5}$
(4)$19\sqrt{2}$
(1)$\frac{4}{3}-15\sqrt{2}$
(2)$-6$
(3)$61 + 24\sqrt{5}$
(4)$19\sqrt{2}$
例4 木工师傅采用如图所示的方式,在一块矩形木板上截出面积分别为$18\ dm^{2}$和$32\ dm^{2}$的两块正方形木板。
(1)求剩余木板(阴影部分)的面积;
(2)如果木工师傅想从剩余的木板中截出长为$1.5\ dm$、宽为$1\ dm$的矩形木块,最多能截出____块这样的木块。
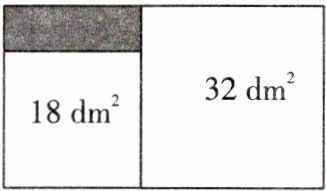
(1)求剩余木板(阴影部分)的面积;
(2)如果木工师傅想从剩余的木板中截出长为$1.5\ dm$、宽为$1\ dm$的矩形木块,最多能截出____块这样的木块。

答案:
【例4】
(1)$6\ dm^{2}$
(2)$2$
(1)$6\ dm^{2}$
(2)$2$
1. [2024·峨眉山期中]下列二次根式中,化简后能与$\sqrt{2}$合并的是( )
A.$\sqrt{\dfrac{1}{2}}$
B.$\sqrt{22}$
C.$\sqrt{20}$
D.$\sqrt{0.2}$
A.$\sqrt{\dfrac{1}{2}}$
B.$\sqrt{22}$
C.$\sqrt{20}$
D.$\sqrt{0.2}$
答案:
1.A
2. 计算$\sqrt{48}-9\sqrt{\dfrac{1}{3}}$的结果是( )
A.$-\sqrt{3}$
B.$\sqrt{3}$
C.$-\dfrac{11\sqrt{3}}{3}$
D.$\dfrac{11\sqrt{3}}{3}$
A.$-\sqrt{3}$
B.$\sqrt{3}$
C.$-\dfrac{11\sqrt{3}}{3}$
D.$\dfrac{11\sqrt{3}}{3}$
答案:
2.B
3. 计算:
(1)$\sqrt{3}+3\sqrt{\dfrac{1}{3}}=$____;
(2)$\sqrt{2}×\sqrt{3}-\sqrt{24}=$____。
(1)$\sqrt{3}+3\sqrt{\dfrac{1}{3}}=$____;
(2)$\sqrt{2}×\sqrt{3}-\sqrt{24}=$____。
答案:
3.
(1)$2\sqrt{3}$
(2)$-\sqrt{6}$
(1)$2\sqrt{3}$
(2)$-\sqrt{6}$
查看更多完整答案,请扫码查看


