第109页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
6. 如图,点 $ A(3, t) $ 在第一象限,射线 $ OA $ 与 $ x $ 轴所夹的锐角为 $ \alpha $,$ \tan \alpha = \frac{3}{2} $,则 $ t $ 的值是______。
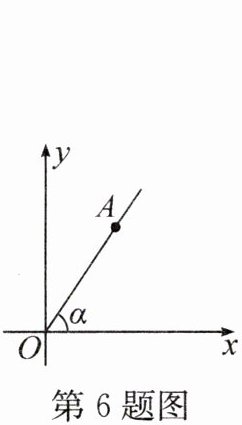

答案:
6. $\frac{9}{2}$
7. [2023·益阳]如图,在平面直角坐标系中,有 $ A(0, 1) $、$ B(4, 1) $、$ C(5, 6) $ 三点,则 $ \sin \angle BAC = $______。
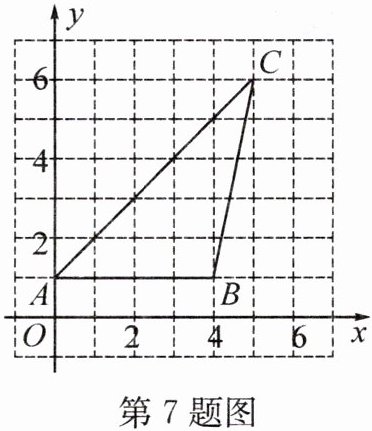

答案:
7. $\frac{\sqrt{2}}{2}$
8. [2024·临夏州]如图,在 $ \triangle ABC $ 中,$ AB = AC = 5 $,$ \sin B = \frac{4}{5} $,则 $ BC $ 的长为______。
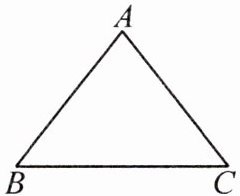

答案:
8. 6
9. (1)若 $ \angle A $ 为锐角,且 $ \sin A = \frac{3}{5} $,求 $ \cos A $、$ \tan A $ 的值;
(2)如图,在 $ Rt \triangle ABC $ 中, $ \angle C = 90° $,$ \tan A = \frac{1}{2} $,求 $ \angle B $ 的正弦值、余弦值。
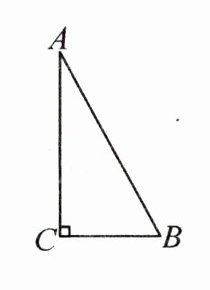
(2)如图,在 $ Rt \triangle ABC $ 中, $ \angle C = 90° $,$ \tan A = \frac{1}{2} $,求 $ \angle B $ 的正弦值、余弦值。

答案:
9.
(1)$\cos A=\frac{4}{5},\tan A=\frac{3}{4}$.
(2)$\sin B=\frac{2\sqrt{5}}{5},\cos B=\frac{\sqrt{5}}{5}$.
(1)$\cos A=\frac{4}{5},\tan A=\frac{3}{4}$.
(2)$\sin B=\frac{2\sqrt{5}}{5},\cos B=\frac{\sqrt{5}}{5}$.
10. (创新意识、推理能力)如图1,根据图中数据完成填空,再按要求答题:
$ \sin^2 A_1 + \sin^2 B_1 = $______,
$ \sin^2 A_2 + \sin^2 B_2 = $______,
$ \sin^2 A_3 + \sin^2 B_3 = $______。
(1)观察上述等式,猜想:在 $ Rt \triangle ABC $ 中, $ \angle C = 90° $,都有 $ \sin^2 A + \sin^2 B = $______;
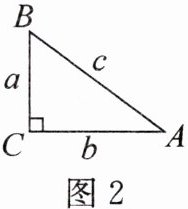
(2)如图2,在 $ Rt \triangle ABC $ 中, $ \angle C = 90° $,$ \angle A $、$ \angle B $、$ \angle C $ 的对边分别是 $ a $、$ b $、$ c $,利用三角函数的定义和勾股定理,证明你的猜想。
]
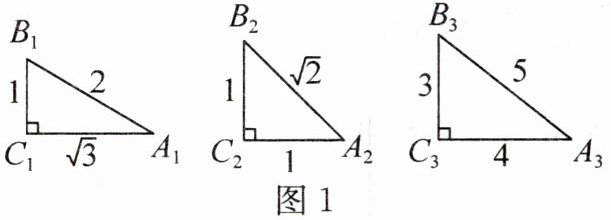
$ \sin^2 A_1 + \sin^2 B_1 = $______,
$ \sin^2 A_2 + \sin^2 B_2 = $______,
$ \sin^2 A_3 + \sin^2 B_3 = $______。
(1)观察上述等式,猜想:在 $ Rt \triangle ABC $ 中, $ \angle C = 90° $,都有 $ \sin^2 A + \sin^2 B = $______;
(2)如图2,在 $ Rt \triangle ABC $ 中, $ \angle C = 90° $,$ \angle A $、$ \angle B $、$ \angle C $ 的对边分别是 $ a $、$ b $、$ c $,利用三角函数的定义和勾股定理,证明你的猜想。
]


答案:
10. 1 1 1
(1)1
(2)略
(1)1
(2)略
查看更多完整答案,请扫码查看


