第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
7. $x$是怎样的实数时,下列二次根式有意义?
(1)$\frac{1}{\sqrt{4 - 3x}}$; (2)$\sqrt{-x^{2}}$;
(3)$\sqrt{1 - x}+\sqrt{x}$; (4)$\frac{\sqrt{1 - 2x}}{x + 1}$.
(1)$\frac{1}{\sqrt{4 - 3x}}$; (2)$\sqrt{-x^{2}}$;
(3)$\sqrt{1 - x}+\sqrt{x}$; (4)$\frac{\sqrt{1 - 2x}}{x + 1}$.
答案:
$7. (1)x<\frac{4}{3} (2)x=0 (3)0\leqslant x\leqslant1$
$(4)x\leqslant\frac{1}{2} $且$ x\neq-1$
$(4)x\leqslant\frac{1}{2} $且$ x\neq-1$
8. [2024·内江校级开学]实数$a$在数轴上对应点的位置如图所示,则化简$\sqrt{a^{2}-8a + 16}+\sqrt{(a - 11)^{2}}$的结果为( )
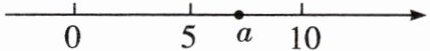
A.$7$
B.$-7$
C.$2a - 15$
D.无法确定
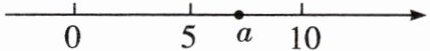
A.$7$
B.$-7$
C.$2a - 15$
D.无法确定
答案:
8. A
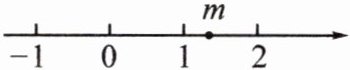
9. [2023·内蒙古]实数$m$在数轴上对应点的位置如图所示,化简:$\sqrt{(m - 2)^{2}}=$____.

答案:
9. 2-m
10. 若$\sqrt{a + b - 5}+\vert3a - b + 1\vert=0$,则$\sqrt{ab}$的负倒数是____.
答案:
$10. -\frac{1}{2}$
11. 若$2$、$5$、$n$为三角形的三边长,化简$\sqrt{(3 - n)^{2}}+\sqrt{(8 - n)^{2}}$.
答案:
11. 5
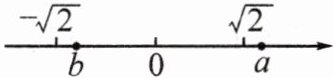
12. 实数$a$、$b$在数轴上对应点的位置如图所示,化简:$\vert a - \sqrt{2}\vert+\vert b + \sqrt{2}\vert-\vert a - b\vert+\sqrt{b^{2}}$.

答案:
12. b
13. 阅读下面解题过程,并回答问题.
化简:$(\sqrt{1 - 3x})^{2}-\vert1 - x\vert$.
解:由隐含条件$1 - 3x\geqslant0$,得$x\leqslant\frac{1}{3}$,
$\therefore1 - x\gt0$,
$\therefore$原式$=(1 - 3x)-(1 - x)=1 - 3x - 1 + x=-2x$.
参照上面的解法,化简:$\sqrt{(x - 3)^{2}}-(\sqrt{2 - x})^{2}$.
化简:$(\sqrt{1 - 3x})^{2}-\vert1 - x\vert$.
解:由隐含条件$1 - 3x\geqslant0$,得$x\leqslant\frac{1}{3}$,
$\therefore1 - x\gt0$,
$\therefore$原式$=(1 - 3x)-(1 - x)=1 - 3x - 1 + x=-2x$.
参照上面的解法,化简:$\sqrt{(x - 3)^{2}}-(\sqrt{2 - x})^{2}$.
答案:
13. 1
查看更多完整答案,请扫码查看


