第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
14. [2024 秋·杏花岭区月考]将边长分别为$1$、$1+\sqrt{2}$、$1 + 2\sqrt{2}$、$1 + 3\sqrt{2}$的正方形的面积记为$S_{1}$、$S_{2}$、$S_{3}$、$S_{4}$.
(1)计算:$S_{2}-S_{1}$、$S_{3}-S_{2}$、$S_{4}-S_{3}$.
(2)把边长为$1+(n - 1)\sqrt{2}$的正方形的面积记作$S_{n}$,其中$n$是正整数,根据(1)中计算的结果,你能猜出$S_{n + 1}-S_{n}$等于多少吗?并说明理由.
(3)若将边长变为$a$、$a+\sqrt{b}$、$a + 2\sqrt{b}$、$a + 3\sqrt{b}$时,则$S_{n + 1}-S_{n}$的值是多少?
(1)计算:$S_{2}-S_{1}$、$S_{3}-S_{2}$、$S_{4}-S_{3}$.
(2)把边长为$1+(n - 1)\sqrt{2}$的正方形的面积记作$S_{n}$,其中$n$是正整数,根据(1)中计算的结果,你能猜出$S_{n + 1}-S_{n}$等于多少吗?并说明理由.
(3)若将边长变为$a$、$a+\sqrt{b}$、$a + 2\sqrt{b}$、$a + 3\sqrt{b}$时,则$S_{n + 1}-S_{n}$的值是多少?
答案:
14.
(1)$S_2 - S_1 = 2 + 2\sqrt{2}$;$S_3 - S_2 = 6 + 2\sqrt{2}$;
$S_4 - S_3 = 10 + 2\sqrt{2}$.
(2)$S_{n + 1} - S_n = 4n - 2 + 2\sqrt{2}$.
(3)$2nb - b + 2a\sqrt{b}$
(1)$S_2 - S_1 = 2 + 2\sqrt{2}$;$S_3 - S_2 = 6 + 2\sqrt{2}$;
$S_4 - S_3 = 10 + 2\sqrt{2}$.
(2)$S_{n + 1} - S_n = 4n - 2 + 2\sqrt{2}$.
(3)$2nb - b + 2a\sqrt{b}$
综合与实践:探究两个正数之和与这两个正数之积的算术平方根的两倍之间的关系.
【探究发现】
$6 + 6 = 2\sqrt{6× 6}=12$;
$\dfrac{1}{5}+\dfrac{1}{5}=2\sqrt{\dfrac{1}{5}×\dfrac{1}{5}}=\dfrac{2}{5}$;
$0.3 + 0.3 = 2\sqrt{0.3× 0.3}=0.6$;
$\dfrac{1}{3}+3>2\sqrt{\dfrac{1}{3}× 3}=2$;
$0.2 + 3.2>2\sqrt{0.2× 3.2}=1.6$;
$\dfrac{1}{3}+\dfrac{1}{27}>2\sqrt{\dfrac{1}{3}×\dfrac{1}{27}}=\dfrac{2}{9}$.
【猜想结论】
若$a>0$,$b>0$,则有$a + b\geqslant 2\sqrt{ab}$(当且仅当$a = b$时,等号成立).
【证明结论】
$\because(\sqrt{a}-\sqrt{b})^{2}\geqslant 0$,
$\therefore$①当且仅当$\sqrt{a}-\sqrt{b}=0$,即$a = b$时,$a - 2\sqrt{ab}+b = 0$,即$a + b = 2\sqrt{ab}$;
②当$\sqrt{a}-\sqrt{b}\neq 0$,即$a\neq b$时,$a - 2\sqrt{ab}+b>0$,即$a + b>2\sqrt{ab}$.
综合上述,若$a>0$,$b>0$,则有$a + b\geqslant 2\sqrt{ab}$(当且仅当$a = b$时,等号成立).
【应用结论】
(1)对于函数$y = x+\dfrac{1}{x}(x>0)$,当$x$取何值时,$y$的值最小?最小值是多少?
(2)对于函数$y=\dfrac{1}{x - 5}+x(x>5)$,当$x$取何值时,$y$的值最小?最小值是多少?
【拓展应用】
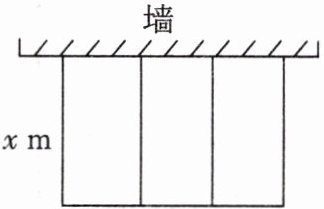
(3)如图,学校计划一边靠墙,其余边用篱笆围成三小块面积均为$24\space m^{2}$的矩形苗圃,中间用两道篱笆隔断.设每小块苗圃垂直于墙的一边长为$x\space m$,当$x$为何值时,所用篱笆的总长度最短?最短长度是多少?
【探究发现】
$6 + 6 = 2\sqrt{6× 6}=12$;
$\dfrac{1}{5}+\dfrac{1}{5}=2\sqrt{\dfrac{1}{5}×\dfrac{1}{5}}=\dfrac{2}{5}$;
$0.3 + 0.3 = 2\sqrt{0.3× 0.3}=0.6$;
$\dfrac{1}{3}+3>2\sqrt{\dfrac{1}{3}× 3}=2$;
$0.2 + 3.2>2\sqrt{0.2× 3.2}=1.6$;
$\dfrac{1}{3}+\dfrac{1}{27}>2\sqrt{\dfrac{1}{3}×\dfrac{1}{27}}=\dfrac{2}{9}$.
【猜想结论】
若$a>0$,$b>0$,则有$a + b\geqslant 2\sqrt{ab}$(当且仅当$a = b$时,等号成立).
【证明结论】
$\because(\sqrt{a}-\sqrt{b})^{2}\geqslant 0$,
$\therefore$①当且仅当$\sqrt{a}-\sqrt{b}=0$,即$a = b$时,$a - 2\sqrt{ab}+b = 0$,即$a + b = 2\sqrt{ab}$;
②当$\sqrt{a}-\sqrt{b}\neq 0$,即$a\neq b$时,$a - 2\sqrt{ab}+b>0$,即$a + b>2\sqrt{ab}$.
综合上述,若$a>0$,$b>0$,则有$a + b\geqslant 2\sqrt{ab}$(当且仅当$a = b$时,等号成立).
【应用结论】
(1)对于函数$y = x+\dfrac{1}{x}(x>0)$,当$x$取何值时,$y$的值最小?最小值是多少?
(2)对于函数$y=\dfrac{1}{x - 5}+x(x>5)$,当$x$取何值时,$y$的值最小?最小值是多少?
【拓展应用】
(3)如图,学校计划一边靠墙,其余边用篱笆围成三小块面积均为$24\space m^{2}$的矩形苗圃,中间用两道篱笆隔断.设每小块苗圃垂直于墙的一边长为$x\space m$,当$x$为何值时,所用篱笆的总长度最短?最短长度是多少?

答案:
(1)当$x = 1$时,y的值最小,最小值是2.
(2)当$x = 6$时,y的值最小,最小值是7.
(3)当x为$3\sqrt{2}$米时,所用篱笆总长度最短,最短长度为$24\sqrt{2}m$.
(1)当$x = 1$时,y的值最小,最小值是2.
(2)当$x = 6$时,y的值最小,最小值是7.
(3)当x为$3\sqrt{2}$米时,所用篱笆总长度最短,最短长度为$24\sqrt{2}m$.
查看更多完整答案,请扫码查看


