《2025年全效学习学业评价方案九年级数学上册华师大版》

相似多边形
定 义:两个边数相同的多边形,如果各边
______________,各角____________,
就称这两个多边形相似.
性 质:相似多边形的对应角________,对应
边成比例.
相似比:相似多边形对应边的比称为________.

答案： 对应成比例 对应相等 相等 相似比

例1 如图,梯形ABCD与梯形A'B'C'D'
相似,A、B、C、D的对应点分别为A'、B'、C'、
D',则α=________°,,β=______°,x=______,
y=______,z=______.

答案： 【例1】118 70 6 12 6

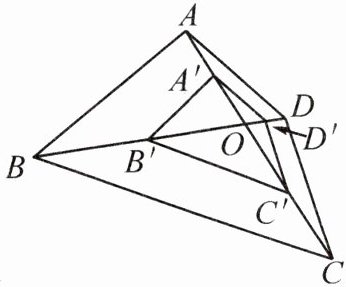
例2 如图,四边形ABCD的对角线相
交于点O,A'、B'、C'、D'分别是OA、OB、OC、OD的中点，试判断四边形ABCD与四边形A'B'C'D'是否相似,并说明理由.

答案： 【例2】相似.
证明：
∵A'、B'、C'、D'分别是OA、OB、OC、OD的中点，
∴A'B'是△OAB的中位线，B'C'是△OBC的中位线，C'D'是△OCD的中位线，D'A'是△ODA的中位线，
∴A'B' = $\frac{1}{2}$AB，B'C' = $\frac{1}{2}$BC，C'D' = $\frac{1}{2}$CD，D'A' = $\frac{1}{2}$DA，
且A'B'//AB，B'C'//BC，C'D'//CD，D'A'//DA，
∴∠OA'B' = ∠OAB，∠OA'D' = ∠OAD，∠OB'A' = ∠OBA，∠OB'C' = ∠OBC，∠OC'B' = ∠OCB，∠OC'D' = ∠OCD，∠OD'C' = ∠ODC，∠OD'A' = ∠ODA，
∴∠D'A'B' = ∠DAB，∠A'B'C' = ∠ABC，∠B'C'D' = ∠BCD，∠C'D'A' = ∠CDA，
∵$\frac{A'B'}{AB} = \frac{B'C'}{BC} = \frac{C'D'}{CD} = \frac{D'A'}{DA} = \frac{1}{2}$，且对应角相等，
∴四边形ABCD与四边形A'B'C'D'相似.

1.如图所示的各组图形中,相似的是( )

答案： 1.C

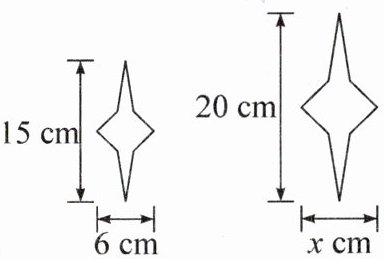
2.如图,有两个相似的星星图案,则x的值为
( )


A.8
B.10
C.12
D.15

答案： 2.A

3.[2024秋.双峰县期末]如图,已知两个四
边形相似,则可以确定α=______°,x=
______.

答案： 3. 60 2

1.四边形ABCD的四条边长分别为54cm、
48cm、45cm、63cm,一个和它相似的四边
形的最短边长为15cm,则这个四边形的最
长边长为 ( )

A.18cm
B.16cm
C.21cm
D.24cm

答案： 1.C

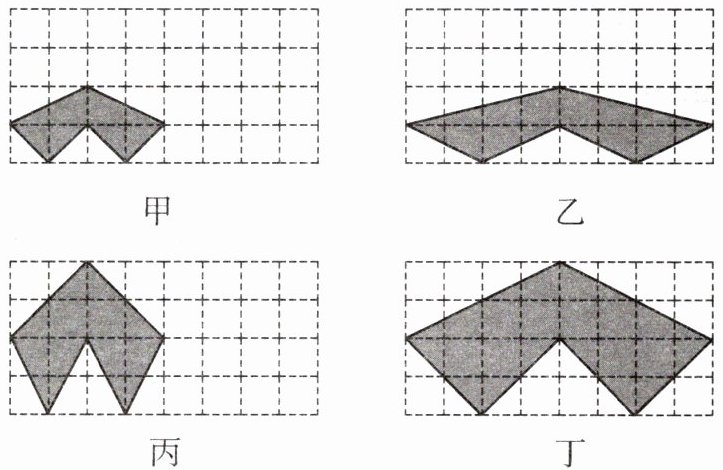
2.[2024.连云港]下列网格中各个小正方形
的边长均为1,阴影部分图形分别记作甲、
乙、丙、丁,其中是相似图形的为 ( )


A.甲和乙
B.乙和丁
C.甲和丙
D.甲和丁

答案： 2.D