第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. [2024 南通] 计算$\sqrt{27} × \sqrt{\frac{1}{3}}$的结果是(
A.9
B.3
C.$3\sqrt{3}$
D.$\sqrt{3}$
B
)A.9
B.3
C.$3\sqrt{3}$
D.$\sqrt{3}$
答案:
B
2. 母题 教材 P109 习题 T1 下列计算正确的是(
A.$\sqrt{2} × \sqrt{3} = \sqrt{5}$
B.$\sqrt{24} × \sqrt{\frac{3}{2}} = 6$
C.$\sqrt{30} ÷ \sqrt{6} = 5$
D.$\sqrt{\frac{4}{7}} ÷ \sqrt{\frac{1}{49}} = 7\sqrt{2}$
B
)A.$\sqrt{2} × \sqrt{3} = \sqrt{5}$
B.$\sqrt{24} × \sqrt{\frac{3}{2}} = 6$
C.$\sqrt{30} ÷ \sqrt{6} = 5$
D.$\sqrt{\frac{4}{7}} ÷ \sqrt{\frac{1}{49}} = 7\sqrt{2}$
答案:
B
3. 估计$4\sqrt{2} × \sqrt{7} + 1$的值在(
A.14 到 14.5 之间
B.14.5 到 15 之间
C.15 到 15.5 之间
D.15.5 到 16 之间
D
)A.14 到 14.5 之间
B.14.5 到 15 之间
C.15 到 15.5 之间
D.15.5 到 16 之间
答案:
D
4. 新考法 数形结合法 如图,长方形内有两个相邻的正方形,其面积分别为 6 和 24,则图中阴影部分的面积为(
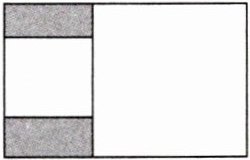
A.5
B.$5\sqrt{5}$
C.6
D.$6\sqrt{6}$
C
)
A.5
B.$5\sqrt{5}$
C.6
D.$6\sqrt{6}$
答案:
C 【点拨】设两个正方形的边长是x,y(0<x<y),则x²=6,y²=24,
∴x=√6,y=√24.
∴阴影部分的面积为(y-x)x=(√24-√6)×√6=6.
∴x=√6,y=√24.
∴阴影部分的面积为(y-x)x=(√24-√6)×√6=6.
5. [2025 石家庄鹿泉区模拟] 若$\sqrt{2}x + \sqrt{2}y + \sqrt{2}z = \sqrt{6}$,则$2x + 2y + 2z$的值为(
A.$\sqrt{3}$
B.$\sqrt{6}$
C.$2\sqrt{3}$
D.$2\sqrt{6}$
C
)A.$\sqrt{3}$
B.$\sqrt{6}$
C.$2\sqrt{3}$
D.$2\sqrt{6}$
答案:
C 【点拨】
∵√2x+√2y+√2z=√6,
∴√2(x+y+z)=√6.
∴x+y+z=√3.
∴2x+2y+2z=2(x+y+z)=2√3.故选C.
∵√2x+√2y+√2z=√6,
∴√2(x+y+z)=√6.
∴x+y+z=√3.
∴2x+2y+2z=2(x+y+z)=2√3.故选C.
6. 分母有理化:$\frac{1}{\sqrt{a - b}} = $
$\frac{\sqrt{a - b}}{a - b}$
(其中$a - b > 0$)。
答案:
√(a-b)/(a-b)
7. 新趋势 学科内综合 已知不等式$2\sqrt{2}x - \sqrt{6} > 0$,则这个不等式的解集为
x>√3/2
。
答案:
x>√3/2
8. 新视角 结论开放题 若一个无理数$a与\sqrt{8}$的积是一个有理数,写出$a$的一个值是
√2(答案不唯一)
。
答案:
√2(答案不唯一)
9. 比较大小:
$\frac{5}{\sqrt{3}}$
$\frac{5}{\sqrt{3}}$
>
$\sqrt{3}$,$-\sqrt{18}$ >
$-\frac{9}{\sqrt{3}}$。
答案:
>;> 【点拨】
∵5/√3=5√3/3,5√3/3>√3,
∴5/√3>√3.
∵-9/√3=-3√3,-√18=-3√2,3√3>3√2,
∴-√18>-9/√3.
∵5/√3=5√3/3,5√3/3>√3,
∴5/√3>√3.
∵-9/√3=-3√3,-√18=-3√2,3√3>3√2,
∴-√18>-9/√3.
10. 若$mn > 0$,$m + n < 0$,则化简$\sqrt{mn} ÷ \sqrt{\frac{n}{m}} = $
-m
。
答案:
-m 【点拨】
∵mn>0,m+n<0,
∴m<0,n<0.
∴√(mn)÷√(n/m)=√(mn÷n/m)=√(mn·m/n)=√(m²)=-m.
∵mn>0,m+n<0,
∴m<0,n<0.
∴√(mn)÷√(n/m)=√(mn÷n/m)=√(mn·m/n)=√(m²)=-m.
11. [2025 衡水月考] 若$\sqrt{2} × \sqrt{20} = \sqrt{2} × m\sqrt{5} = m\sqrt{n}$,则$m - n = $
-8
。
答案:
-8 【点拨】
∵√2×√20=√2×2√5=2√10,
∴m=2,n=10.
∴m-n=2-10=-8.
∵√2×√20=√2×2√5=2√10,
∴m=2,n=10.
∴m-n=2-10=-8.
12. 母题 教材 P109 习题 T2 计算:
(1)$\frac{1}{3}\sqrt{27} × \frac{1}{2}\sqrt{12}$;
(2)$\sqrt{75} × \sqrt{32} ÷ \sqrt{12}$;
(3)$\sqrt{1\frac{1}{3}} ÷ \sqrt{2\frac{1}{3}} ÷ \sqrt{1\frac{2}{5}}$。
(1)$\frac{1}{3}\sqrt{27} × \frac{1}{2}\sqrt{12}$;
(2)$\sqrt{75} × \sqrt{32} ÷ \sqrt{12}$;
(3)$\sqrt{1\frac{1}{3}} ÷ \sqrt{2\frac{1}{3}} ÷ \sqrt{1\frac{2}{5}}$。
答案:
【解】
(1)原式=√3×√3=3.
(2)原式=5√3×4√2÷2√3=(5×4÷2)√(3×2÷3)=10√2.
(3)原式=√(4/3)÷√(7/3)÷√(7/5)=√(4/3×3/7×5/7)=2√5/7.
(1)原式=√3×√3=3.
(2)原式=5√3×4√2÷2√3=(5×4÷2)√(3×2÷3)=10√2.
(3)原式=√(4/3)÷√(7/3)÷√(7/5)=√(4/3×3/7×5/7)=2√5/7.
13. 新趋势 跨学科综合 电流通过导线时会产生热量,电流$I$(单位:A)、导线电阻$R$(单位:$\Omega$)、通电时间$t$(单位:s)与产生的热量$Q$(单位:J)满足$Q = I^2Rt$。已知导线的电阻为$2\Omega$,1 s 内导线产生 50 J 的热量,则电流$I$为(
A.2 A
B.5 A
C.8 A
D.10 A
B
)A.2 A
B.5 A
C.8 A
D.10 A
答案:
B
14. 如果$ab > 0$,$a + b < 0$,那么下面各式:①$\sqrt{\frac{a}{b}} \cdot \sqrt{\frac{b}{a}} = 1$;②$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$;③$\sqrt{ab} ÷ \sqrt{\frac{a}{b}} = -b$,其中正确的是(
A.①②
B.①③
C.②③
D.①②③
B
)A.①②
B.①③
C.②③
D.①②③
答案:
B 【点拨】
∵ab>0,a+b<0,
∴a<0,b<0.
∴√(a/b)·√(b/a)=1,√(a/b)=√(-a)/√(-b),√(ab)÷√(a/b)=-b.
∵ab>0,a+b<0,
∴a<0,b<0.
∴√(a/b)·√(b/a)=1,√(a/b)=√(-a)/√(-b),√(ab)÷√(a/b)=-b.
查看更多完整答案,请扫码查看


