第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. [2025 石家庄新华区月考]下列各组中的两个图形中,属于全等图形的是(

C
)
答案:
C
2. 下列不是利用三角形的稳定性的是(
A.自行车的三脚架
B.三角形的房架
C.照相机的支架
D.门框的长方形架
D
)A.自行车的三脚架
B.三角形的房架
C.照相机的支架
D.门框的长方形架
答案:
D
3. 如图,一块三角形的玻璃打碎成 4 块,现要到玻璃店去配一块完全一样的玻璃,小荣说最简单的办法是只需要带④去,小荣作出这判断的依据是(

A.AAS
B.SSS
C.SAS
D.ASA
D
)
A.AAS
B.SSS
C.SAS
D.ASA
答案:
D
4. 如图,$\triangle ABC≌\triangle FDE$,$\angle C = 40^{\circ}$,$\angle F = 110^{\circ}$,则$\angle B$等于(

A.$20^{\circ}$
B.$30^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
B
)
A.$20^{\circ}$
B.$30^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
答案:
B
5. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AD平分\angle CAB$,$DE\perp AB于点E$,则下列结论中,不正确的是(
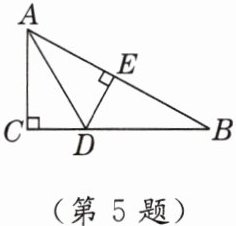
A.$BD + ED = BC$
B.$DE平分\angle ADB$
C.$DA平分\angle EDC$
D.$ED + AC>AD$
B
)
A.$BD + ED = BC$
B.$DE平分\angle ADB$
C.$DA平分\angle EDC$
D.$ED + AC>AD$
答案:
B 【点拨】由已知条件易得△ACD≌△AED,则有CD=ED,∠ADC=∠ADE,所以BD+ED=BD+CD=BC,ED+AC=CD+AC>AD,DA平分∠EDC,故A,C,D正确;无法得出DE平分∠ADB,故B不正确.
6. 如图为 6 个边长相等的正方形的组合图形,则$\angle 1 + \angle 2 + \angle 3 = $(

A.$90^{\circ}$
B.$120^{\circ}$
C.$135^{\circ}$
D.$150^{\circ}$
C
)
A.$90^{\circ}$
B.$120^{\circ}$
C.$135^{\circ}$
D.$150^{\circ}$
答案:
C
7. 荣德原创题 如图,$AB\perp CD$,且$AB = CD$,$E$,$F是AD$上两点,$CE\perp AD$,$BF\perp AD$。若$CE = a$,$BF = b$,$EF = c$,则$AD$的长为(

A.$a + c$
B.$b + c$
C.$a - b + c$
D.$a + b - c$
D
)
A.$a + c$
B.$b + c$
C.$a - b + c$
D.$a + b - c$
答案:
D 【点拨】因为AB⊥CD,CE⊥AD,BF⊥AD,所以∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°. 所以∠A=∠C. 因为∠A=∠C,∠AFB=∠CED=90°,AB=CD,所以△ABF≌△CDE. 所以CE=AF=a,BF=DE=b. 因为EF=c,所以AD=AF+DE-EF=a+b-c.
8. 如图,$AD平分\angle BAC$,且$AD\perp BD于点D$,若$S_{\triangle ABC} = 10$,则$S_{\triangle ADC} = $( )

A.4.5
B.5
C.5.5
D.6

A.4.5
B.5
C.5.5
D.6
答案:
B 【点拨】延长BD交AC于点E,如图所示.
∵AD平分∠BAC,
∴∠BAD=∠EAD.
又
∵AD⊥BD于点D,
∴∠ADB=∠ADE=90°.

在△ABD和△AED中,∠BAD=∠EAD,AD=AD,∠ADB=∠ADE,
∴△ABD≌△AED(ASA).
∴BD=DE.
∴S△ADE=$\frac{1}{2}$S△ABE,S△CDE=$\frac{1}{2}$S△CBE.
∴S△ADC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×10=5,故选B.
B 【点拨】延长BD交AC于点E,如图所示.
∵AD平分∠BAC,
∴∠BAD=∠EAD.
又
∵AD⊥BD于点D,
∴∠ADB=∠ADE=90°.

在△ABD和△AED中,∠BAD=∠EAD,AD=AD,∠ADB=∠ADE,
∴△ABD≌△AED(ASA).
∴BD=DE.
∴S△ADE=$\frac{1}{2}$S△ABE,S△CDE=$\frac{1}{2}$S△CBE.
∴S△ADC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×10=5,故选B.
9. “如果$m$,$n$互为倒数,那么$mn = 1$”的逆命题是
真
命题。
答案:
真
10. 新视角 条件开放题 如图,已知$AB = DE$,$\angle A = \angle D$,请你添加一个条件:

AC=DC(答案不唯一)
,使$\triangle ABC≌\triangle DEC$。
答案:
AC=DC(答案不唯一)
11. 如图,课间小林拿着老师的等腰直角三角板玩,不小心掉到两个凳子之间(凳子与地面垂直),已知$DC = 55\mathrm{cm}$,$CE = 75\mathrm{cm}$,则两个凳子的高度之和为

130
$\mathrm{cm}$。
答案:
130 【点拨】由题意,得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°.
∴∠ACD+∠DAC=∠ACD+∠BCE=90°.
∴∠DAC=∠BCE.
∴△ADC≌△CEB(AAS).
∴CE=AD=75 cm,BE=CD=55 cm.
∴两个凳子的高度之和为AD+BE=75+55=130(cm).
∴∠ADC=∠CEB=90°.
∴∠ACD+∠DAC=∠ACD+∠BCE=90°.
∴∠DAC=∠BCE.
∴△ADC≌△CEB(AAS).
∴CE=AD=75 cm,BE=CD=55 cm.
∴两个凳子的高度之和为AD+BE=75+55=130(cm).
12. 添加辅助线是很多同学感觉比较困难的事情。如图①,在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,$BD$是高,$E是\triangle ABC$外一点,$BE = BA$,$\angle E = \angle C$,若$DE = \frac{2}{5}BD$,$AD = 16$,$BD = 20$,求$\triangle BDE$的面积,同学们可以先思考一下…,小颖思考后认为可以这样添加辅助线:在$BD上截取BF = DE$,连接$AF$(如图②)。根据小颖的提示,聪明的你可以求得:
(1)$\triangle BDE≌$
(2)$\triangle BDE$的面积为

(1)$\triangle BDE≌$
△AFB
;(2)$\triangle BDE$的面积为
64
。
答案:
(1)△AFB 【点拨】
∵∠ABD=180°-∠BDA-∠BAD=90°-∠BAD,∠C=180°-∠ABC-∠BAD=90°-∠BAD,
∴∠ABD=∠C.
∵∠E=∠C,
∴∠ABD=∠E.
在△BDE与△AFB中,BE=AB,∠BED=∠ABF,DE=FB,
∴△BDE≌△AFB(SAS).
(2)64 【点拨】
∵△BDE≌△AFB,
∴S△ABF=S△BDE.
∵S△ABD=$\frac{1}{2}$BD·AD=$\frac{1}{2}$×20×16=160,BF=DE=$\frac{2}{5}$×20=8,
∴DF=BD-BF=20-8=12.
∴S△AFD=$\frac{1}{2}$×AD·DF=$\frac{1}{2}$×16×12=96.
∴S△ABF=S△ABD-S△AFD,
∴S△BDE=S△ABF=160-96=64.
∵∠ABD=180°-∠BDA-∠BAD=90°-∠BAD,∠C=180°-∠ABC-∠BAD=90°-∠BAD,
∴∠ABD=∠C.
∵∠E=∠C,
∴∠ABD=∠E.
在△BDE与△AFB中,BE=AB,∠BED=∠ABF,DE=FB,
∴△BDE≌△AFB(SAS).
(2)64 【点拨】
∵△BDE≌△AFB,
∴S△ABF=S△BDE.
∵S△ABD=$\frac{1}{2}$BD·AD=$\frac{1}{2}$×20×16=160,BF=DE=$\frac{2}{5}$×20=8,
∴DF=BD-BF=20-8=12.
∴S△AFD=$\frac{1}{2}$×AD·DF=$\frac{1}{2}$×16×12=96.
∴S△ABF=S△ABD-S△AFD,
∴S△BDE=S△ABF=160-96=64.
查看更多完整答案,请扫码查看


