《2025年综合应用创新题典中点八年级数学上册冀教版》

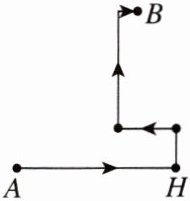
13. 假期中,王强和同学们到某海岛上去探宝旅游,按照探宝图(如图),他们在$A点登陆后先往东走8\sqrt{3}\mathrm{km}到H$点,又往北走$2\sqrt{3}\mathrm{km}$,遇到障碍后又往西走了$3\sqrt{3}\mathrm{km}$,再折向北走了$6\sqrt{3}\mathrm{km}$,往东一拐,再走了$\sqrt{3}\mathrm{km}就找到宝藏埋藏点B$. 问：他们共走了多少千米？

答案： 【解】$8\sqrt {3}+2\sqrt {3}+3\sqrt {3}+6\sqrt {3}+\sqrt {3}=20\sqrt {3}(km)$．答：他们共走了$20\sqrt {3}\ km$．

14. 嘉嘉准备完成题目“$(□\sqrt{\frac{1}{27}}-\frac{2}{3}\sqrt{18})-(\sqrt{\frac{4}{3}}-\sqrt{8})$”时,发现“$□$”处的数印刷不清楚.
(1) 他把“$□$”处的数猜成$6$,请你计算$(6\sqrt{\frac{1}{27}}-\frac{2}{3}\sqrt{18})-(\sqrt{\frac{4}{3}}-\sqrt{8})$的结果；
(2) 他妈妈说：“你猜错了,我看到该题的标准答案是$-\sqrt{3}$.”请你通过计算说明原题中“$□$”处的数是几.
(1)$\left(6\sqrt {\frac {1}{27}}-\frac {2}{3}\sqrt {18}\right)-\left(\sqrt {\frac {4}{3}}-\sqrt {8}\right)=6×\frac {\sqrt {3}}{9}-\frac {2}{3}×3\sqrt {2}-\frac {2\sqrt {3}}{3}+2\sqrt {2}=\frac {2\sqrt {3}}{3}-2\sqrt {2}-\frac {2\sqrt {3}}{3}+2\sqrt {2}=0$．
(2)设原题中“■”处的数为$a$，则$\left(a\sqrt {\frac {1}{27}}-\frac {2}{3}\sqrt {18}\right)-\left(\sqrt {\frac {4}{3}}-\sqrt {8}\right)=a×\frac {\sqrt {3}}{9}-\frac {2}{3}×3\sqrt {2}-\frac {2\sqrt {3}}{3}+2\sqrt {2}=\frac {a\sqrt {3}}{9}-2\sqrt {2}-\frac {2\sqrt {3}}{3}+2\sqrt {2}=\frac {(a-6)\sqrt {3}}{9}=-\sqrt {3}$，解得$a=-3$．故原题中“■”处的数是$-3$．

答案： 【解】
(1)$\left(6\sqrt {\frac {1}{27}}-\frac {2}{3}\sqrt {18}\right)-\left(\sqrt {\frac {4}{3}}-\sqrt {8}\right)=6×\frac {\sqrt {3}}{9}-\frac {2}{3}×3\sqrt {2}-\frac {2\sqrt {3}}{3}+2\sqrt {2}=\frac {2\sqrt {3}}{3}-2\sqrt {2}-\frac {2\sqrt {3}}{3}+2\sqrt {2}=0$．
(2)设原题中“■”处的数为$a$，则$\left(a\sqrt {\frac {1}{27}}-\frac {2}{3}\sqrt {18}\right)-\left(\sqrt {\frac {4}{3}}-\sqrt {8}\right)=a×\frac {\sqrt {3}}{9}-\frac {2}{3}×3\sqrt {2}-\frac {2\sqrt {3}}{3}+2\sqrt {2}=\frac {a\sqrt {3}}{9}-2\sqrt {2}-\frac {2\sqrt {3}}{3}+2\sqrt {2}=\frac {(a-6)\sqrt {3}}{9}=-\sqrt {3}$，解得$a=-3$．故原题中“■”处的数是$-3$．

16. 新考法待定系数法先阅读材料,再解答问题.
已知$a$,$b$都是有理数,且满足$a+\sqrt{2}b = 3 - 2\sqrt{2}$,求$b^a$的值.
解：由题意得$(a - 3)+(b + 2)\sqrt{2}= 0$.
$\because a$,$b$都是有理数,$\therefore a - 3$,$b + 2$也是有理数.
又$\because\sqrt{2}$是无理数,$\therefore a - 3 = 0$,$b + 2 = 0$.
$\therefore a = 3$,$b = - 2$. $\therefore b^a = (- 2)^3 = - 8$.
问题：已知$x$,$y$都是有理数,且满足$x^2 - 2y+\sqrt{5}y = 8 + 4\sqrt{5}$,求$x + y$的值.

答案： 【解】$\because x^{2}-2y+\sqrt {5}y=8+4\sqrt {5}$，$\therefore (x^{2}-2y-8)+(y-4)\sqrt {5}=0$．$\because x$，$y$都是有理数，$\therefore x^{2}-2y-8$，$y-4$也是有理数．又$\because \sqrt {5}$是无理数，$\therefore x^{2}-2y-8=0$，$y-4=0$，解得$x=\pm 4$，$y=4$．当$x=4$，$y=4$时，$x+y=4+4=8$；当$x=-4$，$y=4$时，$x+y=(-4)+4=0$．综上，$x+y$的值是$8$或$0$．