《2025年综合应用创新题典中点八年级数学上册冀教版》

1. [2025 保定模拟]若 $ 2\sqrt{5} $ 与 $ \sqrt{m} $ 可以合并,则 $ m $ 的值可以为(D)
A.15
B.25
C.30
D.45

答案： D

2. 下列运算,结果正确的是(D)
A.$ \sqrt{2}+\sqrt{3}= \sqrt{5} $
B.$ 3\sqrt{5}-\sqrt{5}= 3 $
C.$ \frac{\sqrt{8}}{2}= \sqrt{4} $
D.$ \sqrt{6} × \sqrt{2}= 2\sqrt{3} $

答案： D

3. 设 $ m= \sqrt{45}-5\sqrt{\frac{1}{5}} $,则实数 $ m $ 的取值范围是(A)
A.$ 4＜m＜5 $
B.$ 3＜m＜4 $
C.$ m＜3 $
D.$ m＞5 $

答案： A

4. 玲玲在完成计算题 $ (1+\sqrt{2})□(1-\sqrt{2}) $ 时,发现“$ □ $”处的符号模糊不清,同桌洋洋告诉她,答案为有理数,则“$ □ $”处的符号为(A)
A.$ + $ 或 $ × $
B.$ + $ 或 $ ÷ $
C.$ - $ 或 $ × $
D.$ - $ 或 $ ÷ $

答案： A

5. 在 $ \triangle ABC $ 中,已知 $ AB= \sqrt{3}+\sqrt{2} $,$ BC= \sqrt{3}-\sqrt{2} $,则 $ AC $ 可以是(C)
A.1
B.2
C.3
D.4

答案： C

6. 若 $ 6-\sqrt{13} $ 的整数部分为 $ x $,小数部分为 $ y $,则 $ (2x+\sqrt{13})y $ 的值是(B)
A.$ 5-3\sqrt{13} $
B.3
C.$ 3\sqrt{13}-5 $
D.$ -3 $

答案： B

7. 已知 $ a= \frac{1}{2-\sqrt{3}} $,$ b= \frac{1}{2+\sqrt{3}} $,则 $ a $ 与 $ b $ 的关系是(C)
A.$ a-b= 0 $
B.$ a+b= 0 $
C.$ ab= 1 $
D.$ a^{2}= b^{2} $

答案： C

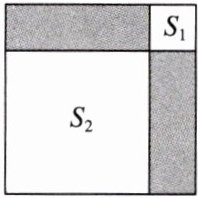
8. 如图,从一个大正方形中截去面积为 $ S_{1} $ 和 $ S_{2} $ 的两个小正方形,若阴影部分的周长和面积分别是 $ 4\sqrt{3}+8\sqrt{6} $ 和 $ 12\sqrt{2} $,则 $ S_{1}+S_{2}= $(C)

A.24
B.$ 24\sqrt{3} $
C.27
D.$ 27\sqrt{3} $

答案： C 【点拨】设面积为S₁和S₂的两个小正方形的边长分别为a,b,则S₁=a²,S₂=b²,根据题意可知,2ab=12√2,4a+4b=4√3+8√6,即a+b=√3+2√6,由(a+b)²=a²+2ab+b²,得a²+b²=(a+b)²-2ab=(√3+2√6)²-12√2=3+12√2+24-12√2=27,
∴S₁+S₂=27,故选C.

9. 已知 $ \sqrt{5}= a $,则 $ 5\sqrt{\frac{1}{5}}-\frac{5}{4}\sqrt{\frac{4}{5}}+\sqrt{45}= $$\frac{7}{2}a$(用含 $ a $ 的代数式表示).

答案： $\frac{7}{2}a$

10. 已知 $ x+y= 2\sqrt{3}+\sqrt{2} $,$ xy= 1-\sqrt{6} $,则 $ x^{2}y+xy^{2} $ 的值为______.

答案： $-5\sqrt{2}$

11. 新考法 新定义计算法 对于任意不相等的两个数 $ a,b $,定义一种运算 $ ※ $ 如下：$ a※b= \frac{\sqrt{a+b}}{a-b} $,如 $ 5※4= \frac{\sqrt{5+4}}{5-4}= 3 $,那么 $ (2-\sqrt{3})※(7※5)= $$\frac{-\sqrt{2}+\sqrt{6}}{4}$.

答案： $\frac{-\sqrt{2}+\sqrt{6}}{4}$ 【点拨】
∵7※5=$\frac{\sqrt{7+5}}{7-5}=\frac{2\sqrt{3}}{2}=\sqrt{3}$,
∴(2-$\sqrt{3}$)※(7※5)=(2-$\sqrt{3}$)※$\sqrt{3}$=$\frac{\sqrt{2-\sqrt{3}}+\sqrt{3}}{2-\sqrt{3}-\sqrt{3}}=\frac{\sqrt{2}}{2-2\sqrt{3}}=\frac{\sqrt{2}(1+\sqrt{3})}{2(1-\sqrt{3})(1+\sqrt{3})}=\frac{-\sqrt{2}+\sqrt{6}}{4}$.

12. 新考向 数学文化 斐波那契(1175～1250 年)是意大利数学家,他研究了一列数,被称为斐波那契数列. 在实际生活中,很多花朵(如梅花,飞燕草等)的瓣数恰好是斐波那契数列中的数. 斐波那契数列中的第 $ n $ 个数可以用 $ \frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}] $ 表示,斐波那契数中的第 4 个数是______3.

答案： 3 【点拨】把n=4代入$\frac{1}{\sqrt{5}}\left[ \left( \frac{1+\sqrt{5}}{2} \right)^n - \left( \frac{1-\sqrt{5}}{2} \right)^n \right]$,可得:$\frac{1}{\sqrt{5}} × \left[ \left( \frac{1+\sqrt{5}}{2} \right)^4 - \left( \frac{1-\sqrt{5}}{2} \right)^4 \right]=\frac{1}{\sqrt{5}} × \left[ \left( \frac{1+\sqrt{5}}{2} \right)^2 \left( \frac{1-\sqrt{5}}{2} \right)^2 \right] × \left[ \left( \frac{1+\sqrt{5}}{2} \right)^2 - \left( \frac{1-\sqrt{5}}{2} \right)^2 \right]=\frac{1}{\sqrt{5}} × \left( \frac{1+2\sqrt{5}+5}{4}+\frac{1-2\sqrt{5}+5}{4} \right) × \left( \frac{6+2\sqrt{5}}{4}-\frac{6-2\sqrt{5}}{4} \right)=\frac{1}{\sqrt{5}} × 3 × \sqrt{5}=3$.

13.(10 分)计算：
(1)$ \sqrt{48} ÷ \sqrt{3}-\sqrt{\frac{1}{2}} × \sqrt{12}+\sqrt{24} $；
(2)$ (\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})-(\sqrt{2}-\sqrt{10})^{2} $.

答案： 【解】
(1)原式=4$\sqrt{3}$÷$\sqrt{3}$-$\sqrt{6}$+2$\sqrt{6}$=4+$\sqrt{6}$.
(2)原式=5-3-(2+10-4$\sqrt{5}$)=5-3-12+4$\sqrt{5}$=-10+4$\sqrt{5}$.