第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 真实情境题 体育赛事 如图是巴黎奥运会和残奥会的吉祥物“弗里热”图片,与该图片是全等形的是(

D
)
答案:
D
2. 如图,$\triangle AOC\cong\triangle BOD$.已知$\angle A与\angle B$是对应角,则下列各项判断错误的是(

A.对应角:$\angle OCA与\angle ODB$
B.对应角:$\angle AED与\angle BEC$
C.对应边:$OA与OB$
D.对应边:$AC与BD$
B
)
A.对应角:$\angle OCA与\angle ODB$
B.对应角:$\angle AED与\angle BEC$
C.对应边:$OA与OB$
D.对应边:$AC与BD$
答案:
B
3. 新考向 传统文化 榫卯结构是我国古代建筑、家具及其他木制器械的主要结构方式.如图,将两块全等的木楔($\triangle ABC\cong\triangle DEF$)水平钉入长为$10cm$的长方形木条中(点$B,C,F,E$在同一条直线上).若$CF= 2cm$,则木楔$BC$的长为(

A.$2cm$
B.$4cm$
C.$6cm$
D.$8cm$
B
)
A.$2cm$
B.$4cm$
C.$6cm$
D.$8cm$
答案:
B
4. [2024 成都]如图,$\triangle ABC\cong\triangle CDE$,若$\angle D= 35^{\circ}$,$\angle ACB= 45^{\circ}$,则$\angle DCE$的度数为
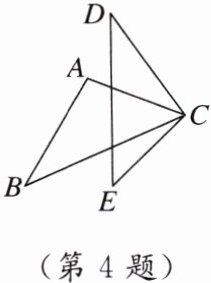
100°
.
答案:
100°
5. 如图,将$\triangle ABC$折叠,使点$A与BC边的中点D$重合,折痕为$MN$,若$AB= 3$,$BC= 2$,则$\triangle DNB$的周长为

4
.
答案:
4 【点拨】
∵ D 为 BC 的中点,且 BC = 2,
∴ BD = $\frac{1}{2}$BC = 1. 由折叠的性质知△ANM≌△DNM,
∴ NA = ND,
∴△DNB 的周长 = ND + NB + BD = NA + NB + BD = AB + BD = 3 + 1 = 4.
∵ D 为 BC 的中点,且 BC = 2,
∴ BD = $\frac{1}{2}$BC = 1. 由折叠的性质知△ANM≌△DNM,
∴ NA = ND,
∴△DNB 的周长 = ND + NB + BD = NA + NB + BD = AB + BD = 3 + 1 = 4.
6. 如图,已知$\triangle ABC\cong\triangle EDF$,点$A,E,C,F$在同一直线上,延长$BC交DF于点M$,若$\angle BAC= 70^{\circ}$,$\angle EDF= 62^{\circ}$,求$\angle CMF$的度数.


答案:
【解】
∵△ABC≌△EDF,
∴∠ACB = ∠F,∠B = ∠EDF = 62°,
∵∠BAC = 70°,
∴∠ACB = 180° - ∠A - ∠B = 180° - 70° - 62° = 48°,
∴∠F = ∠ACB = ∠MCF = 48°,
∴∠CMF = 180° - ∠MCF - ∠F = 84°.
∵△ABC≌△EDF,
∴∠ACB = ∠F,∠B = ∠EDF = 62°,
∵∠BAC = 70°,
∴∠ACB = 180° - ∠A - ∠B = 180° - 70° - 62° = 48°,
∴∠F = ∠ACB = ∠MCF = 48°,
∴∠CMF = 180° - ∠MCF - ∠F = 84°.
7. 新考法 分类讨论法 如图,在四边形$ABCD$中,$\angle ABC= \angle BCD= 90^{\circ}$,点$M,N分别在边BC和边CD$上,且$\triangle ABC与\triangle MCN$全等,$AC与MN$是对应边.若$AB= 3$,$BC= 4$,$CD= 5$,则$DN$的长为(

A.$1$
B.$2或3$
C.$1或2$
D.$3或4$
C
)
A.$1$
B.$2或3$
C.$1或2$
D.$3或4$
答案:
C
8. 如图,在锐角三角形$ABC$中,$F,G分别是AB,AC$上的点,$\triangle ACF\cong\triangle ADF$,$\triangle ABG\cong\triangle AEG$,且$DF// GE$,$BG,CF交于点H$,若$\angle BAC= 40^{\circ}$,则$\angle BHC$的度数是(
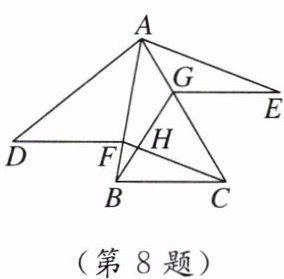
A.$110^{\circ}$
B.$100^{\circ}$
C.$90^{\circ}$
D.$120^{\circ}$
B
)
A.$110^{\circ}$
B.$100^{\circ}$
C.$90^{\circ}$
D.$120^{\circ}$
答案:
B 【点拨】如图,延长 EG 交 AB 于点 Q,交 AD 于点 P,
∵△ACF≌△ADF,△ABG≌△AEG,∠BAC = 40°,
∴∠DAF = ∠BAC = 40°,
∠EAG = ∠BAC = 40°,∠D = ∠ACF,∠E = ∠ABG,
∴∠PAE = 120°,
∴∠APE + ∠E = 60°.
∵DF//EP,
∴∠APE = ∠D,
∴∠APE = ∠ACF,
∴∠ABG + ∠ACF = 60°.
∵∠BFH = ∠BAC + ∠ACF,
∴∠BHC = ∠ABG + ∠BFH = ∠ABG + ∠BAC + ∠ACF = 60° + 40° = 100°,故选 B.
∵△ACF≌△ADF,△ABG≌△AEG,∠BAC = 40°,
∴∠DAF = ∠BAC = 40°,
∠EAG = ∠BAC = 40°,∠D = ∠ACF,∠E = ∠ABG,
∴∠PAE = 120°,
∴∠APE + ∠E = 60°.
∵DF//EP,
∴∠APE = ∠D,
∴∠APE = ∠ACF,
∴∠ABG + ∠ACF = 60°.
∵∠BFH = ∠BAC + ∠ACF,
∴∠BHC = ∠ABG + ∠BFH = ∠ABG + ∠BAC + ∠ACF = 60° + 40° = 100°,故选 B.
9. 新考向 数学文化 如图是我国古代数学家赵爽在注解《周髀算经》时给出的一幅“弦图”,四个全等的直角三角形($Rt\triangle ABE$,$Rt\triangle DAH$,$Rt\triangle CDG$,$Rt\triangle BCF$)和一个小正方形$EFGH恰好拼成一个大正方形ABCD$.若$HG= 1$,$S_{\triangle ABE}= 6$,则正方形$ABCD$的边长为______

5
.
答案:
5 【点拨】由题易知$S_{\triangle ABE}=S_{\triangle ADH}=S_{\triangle CDG}=S_{\triangle CBF}=6$,
∴大正方形 ABCD 的面积为$6 + 6 + 6 + 6 + 1^{2}=24 + 1 = 25$,
∴正方形 ABCD 的边长为 5.
∴大正方形 ABCD 的面积为$6 + 6 + 6 + 6 + 1^{2}=24 + 1 = 25$,
∴正方形 ABCD 的边长为 5.
查看更多完整答案,请扫码查看


